题目内容
已知不等式(2+x)(3-x)≥0的解集为A,函数f(x)=
(k<0)的定义域为B.
(1)求集合A;
(2)若B⊆A,试求实数k的取值范围;
(3)若B=[x1,x2]且x1<x2,又(x1+1)(x2+1)=-4,求x2-x1的值.
| kx2+4x+k+3 |
(1)求集合A;
(2)若B⊆A,试求实数k的取值范围;
(3)若B=[x1,x2]且x1<x2,又(x1+1)(x2+1)=-4,求x2-x1的值.
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:(1)根据不等式的解法即可求集合A;
(2)根据B⊆A,建立条件关系即可求实数k的取值范围;
(3)根据根与系数之间的关系即可求x2-x1的值
(2)根据B⊆A,建立条件关系即可求实数k的取值范围;
(3)根据根与系数之间的关系即可求x2-x1的值
解答:
解:(1)由(2+x)(3-x)≥0得-2≤x≤3,即A=[-2,3].
(2)要使函数有意义,则kx2+4x+k+3≥0,
若B⊆A,设g(x)=kx2+4x+k+3,(k<0),
则满足
,
即
,
解得-4≤k≤-
.
(3)要使函数有意义,则kx2+4x+k+3≥0,
若B=[x1,x2]且x1<x2<0,
则x1,x2是方程kx2+4x+k+3=0的两个根且x1<x2<0,
则x1+x2=-
,x1x2=
,
∵(x1+1)(x2+1)=4,
∴x1x2+x1+x2=3,
即
-
=
=3,
则k=-
.
则x1+x2=-
=8,x1x2=
=-5,
则(x1-x2)2=(x1+x2)2-4x1x2=64-4×(-5)=84,
∵x1<x2,
∴x1-x2<0,
则x1-x2=-
=-2
.
(2)要使函数有意义,则kx2+4x+k+3≥0,
若B⊆A,设g(x)=kx2+4x+k+3,(k<0),
则满足
|
即
|
解得-4≤k≤-
| 3 |
| 2 |
(3)要使函数有意义,则kx2+4x+k+3≥0,
若B=[x1,x2]且x1<x2<0,
则x1,x2是方程kx2+4x+k+3=0的两个根且x1<x2<0,
则x1+x2=-
| 4 |
| k |
| k+3 |
| k |
∵(x1+1)(x2+1)=4,
∴x1x2+x1+x2=3,
即
| k+3 |
| k |
| 4 |
| k |
| k-1 |
| k |
则k=-
| 1 |
| 2 |
则x1+x2=-
| 4 |
| k |
| k+3 |
| k |
则(x1-x2)2=(x1+x2)2-4x1x2=64-4×(-5)=84,
∵x1<x2,
∴x1-x2<0,
则x1-x2=-
| 84 |
| 21 |
点评:本题主要考查集合的基本运算以及函数定义域的求解,综合考查函数的应用.

练习册系列答案
相关题目
设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2}则(∁UA)∩B=( )
| A、{0} |
| B、{-2,-1} |
| C、{0,1,2} |
| D、{1,2} |
函数f(x)=lg(||x2-2x-10|-10|)的零点的个数( )
| A、8 | B、7 | C、6 | D、5 |
钝角△ABC最大边长为4,其余两边长为x,y,以(x,y)为坐标的点所表示的平面区域的面积为( )
| A、4π-8 | ||
| B、4π+8 | ||
| C、4π-6 | ||
D、4π-
|
已知p:-1<2x-3<1,q:x(x-3)<0,则p是q的什么条件( )
| A、必要不充分 |
| B、充分不必要 |
| C、充要 |
| D、既不充分也不必要 |
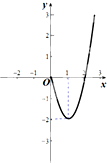 已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.