题目内容
已知各项均为正数的数列{an}的前n项和为Sn,且满足2Sn=an2+an.
(1)求证:{an}为等差数列,并求数列{an}的通项公式;
(2)设bn=2anlog
2an,数列{bn}的前n项和为Hn,求使得Hn+n•2n+1>50成立的最小正整数n.
(1)求证:{an}为等差数列,并求数列{an}的通项公式;
(2)设bn=2anlog
| 1 |
| 2 |
考点:数列的求和,等差数列的前n项和,等差关系的确定
专题:等差数列与等比数列
分析:(1)由2Sn=an2+an,得2Sn-1=an-12+an-1,从而{an}是公差为1的等差数列,由此能求出数列{an}的通项公式.
(2)bn=2anlog
2an=-n•2n,由此利用错位相减法能求出Hn=-n•2n+1+2n+1-2,由此能求出使得Hn+n•2n+1>50成立的最小正整数n.
(2)bn=2anlog
| 1 |
| 2 |
解答:
解:(1)由2Sn=an2+an.①
得2Sn-1=an-12+an-1.②
①-②,得:2an=an2+an-an-12-an-1,
∴an+an-1=an2-an-12,
∴an-an-1=1,
∴{an}是公差为1的等差数列,
由2S1=a12+a1,得a1=1,
∴an=1+(n-1)×1=n.
(2)bn=2anlog
2an=-n•2n,
∴Hn=-(1×2+2×22+3×23+…+n×2n),
∴2Hn=-(22+2×23+3×24+…+n×2n+1),
∴Hn=2+22+23+…+2n-n×2n+1
=
-n×2n-1
=-n•2n+1+2n+1-2,
∵Hn+n•2n+1>50,
∴2n+1>52,
∴n的最小值为5.
得2Sn-1=an-12+an-1.②
①-②,得:2an=an2+an-an-12-an-1,
∴an+an-1=an2-an-12,
∴an-an-1=1,
∴{an}是公差为1的等差数列,
由2S1=a12+a1,得a1=1,
∴an=1+(n-1)×1=n.
(2)bn=2anlog
| 1 |
| 2 |
∴Hn=-(1×2+2×22+3×23+…+n×2n),
∴2Hn=-(22+2×23+3×24+…+n×2n+1),
∴Hn=2+22+23+…+2n-n×2n+1
=
| 2(1-2n) |
| 1-2 |
=-n•2n+1+2n+1-2,
∵Hn+n•2n+1>50,
∴2n+1>52,
∴n的最小值为5.
点评:本题考查数列的通项公式的求法,考查满足条件的n的最小值的求法,是中档题,解题时要注意错位相减求和法的合理运用.

练习册系列答案
相关题目
钝角△ABC最大边长为4,其余两边长为x,y,以(x,y)为坐标的点所表示的平面区域的面积为( )
| A、4π-8 | ||
| B、4π+8 | ||
| C、4π-6 | ||
D、4π-
|
已知p:-1<2x-3<1,q:x(x-3)<0,则p是q的什么条件( )
| A、必要不充分 |
| B、充分不必要 |
| C、充要 |
| D、既不充分也不必要 |
已知复数z=
i-
,则复数
的虚部为( )
| ||
| 2 |
| 1 |
| 2 |
. |
| z |
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
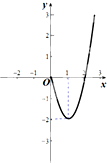 已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.