题目内容
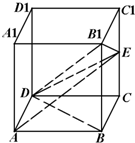 在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.(1)求证:BD⊥AE;
(2)求证:AC∥平面B1DE;
(3)求三棱锥A-B1DE的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)通过证明BD⊥平面AEC,得出BD⊥AE;
(2)通过△ACC1的中位线证明线线平行,再证明线面平行;
(3)点A到平面B1DE的距离等于点C到平面B1DE的距离,利用等积法求出三棱锥A-B1DE的体积.
(2)通过△ACC1的中位线证明线线平行,再证明线面平行;
(3)点A到平面B1DE的距离等于点C到平面B1DE的距离,利用等积法求出三棱锥A-B1DE的体积.
解答:
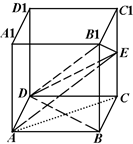
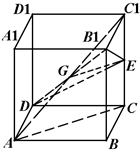
解:(1)证明:连接BD,AE,
∵四边形ABCD是正方形,∴BD⊥AC,
又∵EC⊥底面ABCD,BD?面ABCD,
∴EC⊥BD,且EC∩AC=C,
∴BD⊥平面AEC,
又AE?平面AEC,∴BD⊥AE;-----------(4分)
(2)证明:连接AC1,设AC1∩B1D=G,
则G为AC1的中点,E为C1C的中点,
∴GE为△ACC1的中位线,
∴AC∥GE,GE?平面B1DE,AC?平面B1DE,
∴AC∥平面B1DE;
(3)由(2)知,点A到平面B1DE的距离等于点C到平面B1DE的距离,
∴三棱锥A-B1DE的体积是
V锥A-B1DE=V锥C-B1DE=
S△B1DE•DC=
×(
×1×2)×2=
,
∴三棱锥A-B1DE的体积为
.


解:(1)证明:连接BD,AE,
∵四边形ABCD是正方形,∴BD⊥AC,
又∵EC⊥底面ABCD,BD?面ABCD,
∴EC⊥BD,且EC∩AC=C,
∴BD⊥平面AEC,
又AE?平面AEC,∴BD⊥AE;-----------(4分)
(2)证明:连接AC1,设AC1∩B1D=G,
则G为AC1的中点,E为C1C的中点,
∴GE为△ACC1的中位线,
∴AC∥GE,GE?平面B1DE,AC?平面B1DE,
∴AC∥平面B1DE;
(3)由(2)知,点A到平面B1DE的距离等于点C到平面B1DE的距离,
∴三棱锥A-B1DE的体积是
V锥A-B1DE=V锥C-B1DE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
∴三棱锥A-B1DE的体积为
| 2 |
| 3 |
点评:本题考查了空间中的垂直与平行的判断与性质的应用问题,也考查了求几何体的体积的问题,是综合性题目.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2}则(∁UA)∩B=( )
| A、{0} |
| B、{-2,-1} |
| C、{0,1,2} |
| D、{1,2} |
函数f(x)=lg(||x2-2x-10|-10|)的零点的个数( )
| A、8 | B、7 | C、6 | D、5 |
已知p:-1<2x-3<1,q:x(x-3)<0,则p是q的什么条件( )
| A、必要不充分 |
| B、充分不必要 |
| C、充要 |
| D、既不充分也不必要 |
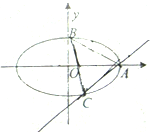 已知椭圆
已知椭圆