题目内容
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x2+3x(x≥0)交于点O,A,与直线x=t(0<t<1)与曲线C1,C2交于B,D
(1)写出四边形ABOD的面积S与t的函数关系S=f(t)
(2)讨论f(t)的单调性,并求f(t)的最大值
(3)对任意t∈(0,1),x∈(
,π],f(t)>cos x+
sin x+a恒成立,求a的取值范围.
(1)写出四边形ABOD的面积S与t的函数关系S=f(t)
(2)讨论f(t)的单调性,并求f(t)的最大值
(3)对任意t∈(0,1),x∈(
| π |
| 4 |
| 3 |
考点:函数恒成立问题,函数解析式的求解及常用方法,利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:(1)先联立两曲线的方程,解出交点B、D的坐标,然后据图可得S=
BD×1,将S表示成关于t的函数;
(2)由(1)知,S=f(t)是一个三次函数,因此利用导数研究其在定义域(0,1)上的单调性;
(3)这是一个两个变量的恒成立问题,只需f(t)min>(cos x+
sin x+a)max,t∈(0,1),x∈(
,π].
| 1 |
| 2 |
(2)由(1)知,S=f(t)是一个三次函数,因此利用导数研究其在定义域(0,1)上的单调性;
(3)这是一个两个变量的恒成立问题,只需f(t)min>(cos x+
| 3 |
| π |
| 4 |
解答:
解:(1)由
解得O(0,0),A(1,1),
将x=t分别代入C1:y=x3(x≥0)与曲线C2:y=-2x2+3x(x≥0)的方程得B(t,t3),D(t,-2t2+3t),
∴BD=-2t2+3t-t3,
∵四边形ABOD的面积是△OBD与△ABD面积的和,
∴S=
BD•t+
BD•(1-t)=
BD×1=
(-2t2+3t-t3)(0<t<1),
=-
t3-t2+
t(0<t<1).

(2)令f(t)=-
t3-t2+
t(0<t<1),
则f′(t)=-
t2-2t+
,
令f′(t)=0得t1=
,或t2=
,
由f′(t)>0得-
<t<
,由f′(t)<0得t<-
或t>
,
∴当t∈(0,
)时,f′(t)>0;当t∈(
,1)时,f′(t)<0;
∴f(t)在(0 ,
)上是增函数,在(
,1)上是减函数,
∴f(x)max=f(
)=
.
(3)由(2)知当t∈(0,1)时,f(t)的最小值是f(0)与f(1)中的较小者,∴f(t)min=f(0)=f(1)=0,
令g(x)=(cos x+
sin x+a)x∈(
,π],
∵g(x)=2(
cosx+
sinx)+a=2sin(x+
)+a,
又∵x∈[
,π],∴当x=
时,g(x)max=2+a,
又∵对任意t∈(0,1),x∈(
,π],f(t)>cos x+
sin x+a恒成立,
∴只需f(t)min>g(x)max,
即0>2+a,∴a<-2.
|
将x=t分别代入C1:y=x3(x≥0)与曲线C2:y=-2x2+3x(x≥0)的方程得B(t,t3),D(t,-2t2+3t),
∴BD=-2t2+3t-t3,
∵四边形ABOD的面积是△OBD与△ABD面积的和,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 2 |

(2)令f(t)=-
| 1 |
| 2 |
| 3 |
| 2 |
则f′(t)=-
| 3 |
| 2 |
| 3 |
| 2 |
令f′(t)=0得t1=
2+
| ||
| -3 |
| ||
| 3 |
由f′(t)>0得-
2+
| ||
| 3 |
| ||
| 3 |
2+
| ||
| 3 |
| ||
| 3 |
∴当t∈(0,
| ||
| 3 |
| ||
| 3 |
∴f(t)在(0 ,
| ||
| 3 |
| ||
| 3 |
∴f(x)max=f(
| ||
| 3 |
29
| ||
| 18 |
(3)由(2)知当t∈(0,1)时,f(t)的最小值是f(0)与f(1)中的较小者,∴f(t)min=f(0)=f(1)=0,
令g(x)=(cos x+
| 3 |
| π |
| 4 |
∵g(x)=2(
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
又∵x∈[
| π |
| 4 |
| π |
| 3 |
又∵对任意t∈(0,1),x∈(
| π |
| 4 |
| 3 |
∴只需f(t)min>g(x)max,
即0>2+a,∴a<-2.
点评:本题的第一问考查利用函数知识解决几何图形的面积问题,应先画出图象,可以看出,因为直线x=t的移动,引起了四边形ABOD面积的变化,因此用t把四边形的面积表示出来,得到S=f(t)的表达式,注意定义域;第二问就是一个利用导数研究三次函数在指定区间上单调性的问题,属常规题;第三问两个变量的取值相互不受影响,因此只需f(t)min>g(x)max,即可,将问题转化为求两个函数的最值问题.

练习册系列答案
相关题目
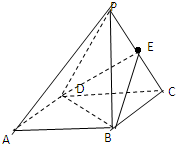 如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,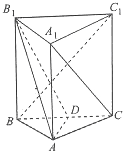 在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.
在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.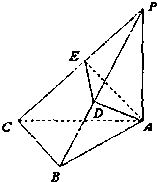 如图,PA⊥平面ABC,AB⊥BC.AD垂直于PB于D,AE垂直于PC于E.PA=
如图,PA⊥平面ABC,AB⊥BC.AD垂直于PB于D,AE垂直于PC于E.PA=