题目内容
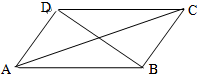
如图，在平行四边形ABCD中，|AB|=3，|BC|=2，| e1 |
| ||
|
|
| e2 |
| ||
|
|
| AB |
| AD |
| π |
| 3 |
（1）若
| AC |
| e1 |
| e2 |
（2）求
| AC |
| BD |
（3）求
| AC |
| BD |
考点：平面向量的综合题
专题：平面向量及应用
分析：（1）由平行四边形法则得
=
+
，而
，
分别是
，
方向上的单位向量，再结合数乘运算、平面向量基本定理中的“唯一性”不难求出x、y；
（2）由题意可以
，
为基底，将
及
用基底表示，再利用内积的定义及运算可求得
•
的值；
（3）直接套用夹角公式cos＜
，
＞=
计算．
| AC |
| AB |
| AD |
| e1 |
| e2 |
| AB |
| AC |
（2）由题意可以
| AB |
| AC |
| AC |
| BD |
| AC |
| BD |
（3）直接套用夹角公式cos＜
| a |
| b |
| ||||
|
|
解答：
解：（1）∵|AB|=3，|BC|=2，
=
，
=
，
∴
=
+
=3
+2
=x
+y
，
∴x=3，y=2．
（2）由向量的运算法则知，
=
-
=2
-3
，
∴
•
=(2
2+3
)•(2
2-3
)=4
2-9
2=-5．
（3）∵
与
的夹角为
，∴
与
的夹角为
，
又|
|=|
|=1，
∴|
|=|
+
|=|2
+3
|=
=
=
，
∴|
|=|
-
|=|2
-3
|=
=
=
，
设
与
的夹角为θ，可得cosθ=
=
=
=-
，
∴
与
的夹角的余弦值为-
．
| e1 |
| ||
|
|
| e2 |
| ||
|
|
∴
| AC |
| AB |
| BC |
| e1 |
| e2 |
| e1 |
| e2 |
∴x=3，y=2．
（2）由向量的运算法则知，
| BD |
| AD |
| AB |
| e2 |
| e1 |
∴
| AC |
| BD |
| e |
| e1 |
| e |
| e1 |
|
| e1 |
（3）∵
| AB |
| AD |
| π |
| 3 |
| e1 |
| e2 |
| π |
| 3 |
又|
| e1 |
| e2 |
∴|
| AC |
| AD |
| AB |
| e2 |
| e1 |
4
|
4+9+12×cos
|
| 19 |
∴|
| BD |
| AD |
| AB |
| e2 |
| e1 |
4
|
4+9-12×cos
|
| 7 |
设
| AC |
| BD |
| ||||
|
|
(2
| ||||||||
|
4
| ||||
|
5
| ||
| 133 |
∴
| AC |
| BD |
5
| ||
| 133 |
点评：利用平面向量基本定理解题，一般先以不共线的、模长及夹角都知道的两个向量作为基底，然后利用基底把已知的、所求的向量表示出来，再进行有关的运算化简和证明；数量积的考查是重点也是热点，一般是距离和角的计算居多，要以数量积的定义为出发点进行思考，要注意结合图形寻找解题思路．
练习册系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
椭圆a2x2-
y2=1的一个焦点是（-2，0），则a等于（ ）
| a |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
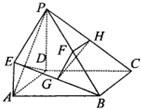如图所示，ABCD是边长为2的正方形，PD⊥平面ABCD，AD=PD=2EA，F，G，H分别为PB，EB，PC的中点．
在Rt△AOB中，