题目内容
从0,1,2,3,4,5,6这7个数字中选出4个不同的数字组成四位数.
(1)一共可以组成多少个四位数;
(2)一共可以组成多少个比1300大的四位数.
(1)一共可以组成多少个四位数;
(2)一共可以组成多少个比1300大的四位数.
考点:排列、组合及简单计数问题
专题:排列组合
分析:(1)0是特殊元素,不能排在首位,需要分步进行,根据分步计数原理可得,
(2)由题意需要分三类,第一类千位比1大的数,第二类千位是1的数,百位比3大的数,第二类千位是1的数,百位是3的数,根据分类计数原理可得.
(2)由题意需要分三类,第一类千位比1大的数,第二类千位是1的数,百位比3大的数,第二类千位是1的数,百位是3的数,根据分类计数原理可得.
解答:
解:(1)分两步,首位不能排0,有
种排法,后面三位从剩下的6个数字中任选3个进行排列,所以共有
•
=720.
答:一共可以组成720个四位数
(2)分三类,第一类千位比1大的数,其它三位任意排,有
•
=600个,
第二类千位是1的数,百位比3大的数,其它两位任意排,有
•
=60个,
第二类千位是1的数,百位是3的数,其它两位任意排,有
=20个,
根据分类计数原理得比1300大的四位数共有600+60+20=680.
答:一共可以组成680个比1300大的四位数.
| A | 1 6 |
| A | 1 6 |
| A | 3 6 |
答:一共可以组成720个四位数
(2)分三类,第一类千位比1大的数,其它三位任意排,有
| A | 1 5 |
| A | 3 6 |
第二类千位是1的数,百位比3大的数,其它两位任意排,有
| A | 1 3 |
| A | 2 5 |
第二类千位是1的数,百位是3的数,其它两位任意排,有
| A | 2 5 |
根据分类计数原理得比1300大的四位数共有600+60+20=680.
答:一共可以组成680个比1300大的四位数.
点评:本题主要考查了分类和分步计算原理的应用,关键审清题意,是分步还是分类.

练习册系列答案
相关题目
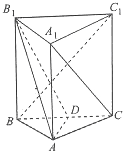 在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.
在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.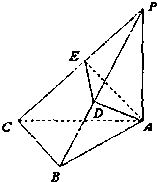 如图,PA⊥平面ABC,AB⊥BC.AD垂直于PB于D,AE垂直于PC于E.PA=
如图,PA⊥平面ABC,AB⊥BC.AD垂直于PB于D,AE垂直于PC于E.PA=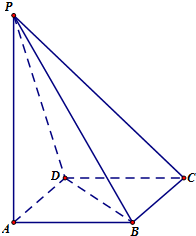 如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,
如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,