题目内容
已知函数f(x)=-
x3+x2+(m2-1)x,(x∈R),其中m>0
(Ⅰ)当m=2时,求曲线y=f(x)在点(3,f(3))处的切线的方程;
(Ⅱ)若f(x)在(
,+∞)上存在单调递增区间,求m的取值范围
(Ⅲ)已知函数f(x)有三个互不相同的零点0,x1,x2且x1<x2,若对任意的x∈[x1,x2],f(x)>f(1)恒成立.求m的取值范围.
| 1 |
| 3 |
(Ⅰ)当m=2时,求曲线y=f(x)在点(3,f(3))处的切线的方程;
(Ⅱ)若f(x)在(
| 3 |
| 2 |
(Ⅲ)已知函数f(x)有三个互不相同的零点0,x1,x2且x1<x2,若对任意的x∈[x1,x2],f(x)>f(1)恒成立.求m的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:(Ⅰ)当m=2时,f(x)=
x3+x2+3x,通过求导得出斜率k的值,从而求出切线方程;
(Ⅱ)只需f′(
)>0即可,解不等式求出即可;
(Ⅲ)由题设可得f(x)=x(-
x2+x+m2-1)=-
x(x-x1)(x-x2),由判别式△>0,求出m的范围,对任意的x∈[x1,x2],f(x)>f(1)恒成立的充要条件是f(1)=m2-
<0,从而综合得出m的取值范围.
| 1 |
| 3 |
(Ⅱ)只需f′(
| 3 |
| 2 |
(Ⅲ)由题设可得f(x)=x(-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:(Ⅰ)当m=2时,f(x)=
x3+x2+3x,
∴f′(x)=-x2+2x+3,
故k=f′(3)=0,
又∵f(3)=9,
∴曲线y=f(x)在点(3,f(3))处的切线方程为:y=9,
(Ⅱ)若f(x)在(
,+∞)上存在单调递增区间,
即存在某个子区间(a,b)?(
,+∞)使得f′(x)>0,
∴只需f′(
)>0即可,
f′(x)=-x2+2x+m2-1,
由f′(
)>0解得m<-
或m>
,
由于m>0,∴m>
.
(Ⅲ)由题设可得f(x)=x(-
x2+x+m2-1)=-
x(x-x1)(x-x2),
∴方程-
x2+x+m2-1=0有两个相异的实根x1,x2,
故x1+x2=3,且△=1+
(m2-1)>0
解得:m<-
(舍去)或m>
,
∵x1<x2,所以2x2>x1+x2=3,∴x2>
>1,
若 x1≤1<x2,
则f(1)=-
(1-x1)(1-x2)≥0,
而f(x1)=0,不合题意.
若1<x1<x2,对任意的x∈[x1,x2],
有x>0,x-x1≥0,x-x2≤0,
则f(x)=-
x(x-x1)(x-x2)≥0,
又f(x1)=0,所以 f(x)在[x1,x2]上的最小值为0,
于是对任意的x∈[x1,x2],f(x)>f(1)恒成立的充要条件是f(1)=m2-
<0,
解得-
<m<
;
综上,m的取值范围是(
,
).
| 1 |
| 3 |
∴f′(x)=-x2+2x+3,
故k=f′(3)=0,
又∵f(3)=9,
∴曲线y=f(x)在点(3,f(3))处的切线方程为:y=9,
(Ⅱ)若f(x)在(
| 3 |
| 2 |
即存在某个子区间(a,b)?(
| 3 |
| 2 |
∴只需f′(
| 3 |
| 2 |
f′(x)=-x2+2x+m2-1,
由f′(
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于m>0,∴m>
| 1 |
| 2 |
(Ⅲ)由题设可得f(x)=x(-
| 1 |
| 3 |
| 1 |
| 3 |
∴方程-
| 1 |
| 3 |
故x1+x2=3,且△=1+
| 4 |
| 3 |
解得:m<-
| 1 |
| 2 |
| 1 |
| 2 |
∵x1<x2,所以2x2>x1+x2=3,∴x2>
| 3 |
| 2 |
若 x1≤1<x2,
则f(1)=-
| 1 |
| 3 |
而f(x1)=0,不合题意.
若1<x1<x2,对任意的x∈[x1,x2],
有x>0,x-x1≥0,x-x2≤0,
则f(x)=-
| 1 |
| 3 |
又f(x1)=0,所以 f(x)在[x1,x2]上的最小值为0,
于是对任意的x∈[x1,x2],f(x)>f(1)恒成立的充要条件是f(1)=m2-
| 1 |
| 3 |
解得-
| ||
| 3 |
| ||
| 3 |
综上,m的取值范围是(
| 1 |
| 2 |
| ||
| 3 |
点评:本题考察了函数的单调性,导数的应用,求切线的方程,解不等式,本题是一道综合题.

练习册系列答案
相关题目
已知复数z1=cosα+isinα和复数z2=cosβ+isinβ,则复数z1•z2的实部是( )
| A、sin(α-β) |
| B、sin(α+β) |
| C、cos(α-β) |
| D、cos(α+β) |
下列命题是真命题的是( )
| A、a>b是ac2>bc2的充要条件 |
| B、a>1,b>1是ab>1的充分条件 |
| C、?x0∈R,e x0≤0 |
| D、若p∨q为真命题,则p∧q为真 |
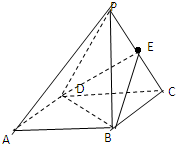 如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,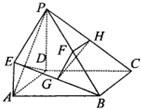 如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图所示,ABCD是边长为2的正方形,PD⊥平面ABCD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.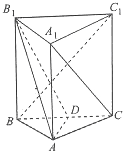 在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.
在三棱柱ABC-A1B1C1中,已知平面BB1C1C⊥平面ABC,AB=AC,D是BC中点,且B1D⊥BC1.