题目内容
（1）已知|
|+2|
|=3，
与
的夹角为60°，
=5
+3
，
=3
+k
，当实数k为何值时
∥
．
（2）不共线向量
，
的夹角为小于120°的角，且|
|=1，|
|=2，已知向量
=
+2
，求|
|的取值范围．
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
（2）不共线向量
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
考点：数量积表示两个向量的夹角,向量的模,平行向量与共线向量
专题：平面向量及应用
分析：（1）由题意可得
、
可以作为平面向量的一个基底，要使
∥
，只需
=
，由此解得k的值．
（2）由＜
，
＞∈（0°，120°），可得
•
∈（-1，2）．求得
2=1-4
•
+16的范围，可得|
|的范围．
| a |
| b |
| c |
| d |
| 5 |
| 3 |
| 3 |
| k |
（2）由＜
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| a |
解答：
解：（1）由题意可得
、
不共线，故
、
可以作为平面向量的一个基底，
∵
=5
+3
，
=3
+k
，要使
∥
，只需
=
，解得 k=
．
（2）∵不共线向量
，
的夹角为小于120°的角，即＜
，
＞∈（0°，120°），
∴cos＜
，
＞∈（-
，1），∴
•
=1×2×cos＜
，
＞∈（-1，2）．
∵向量
=
+2
，∴
2=a2+4
•
+4
2=1-4
•
+16∈（13，25），
∴|
|∈(
，5)．
| a |
| b |
| a |
| b |
∵
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
| 5 |
| 3 |
| 3 |
| k |
| 9 |
| 5 |
（2）∵不共线向量
| a |
| b |
| a |
| b |
∴cos＜
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
∵向量
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| b |
∴|
| a |
| 13 |
点评：本题主要考查两个向量共线的条件，两个向量的数量积的定义，求向量的模，属于中档题．
练习册系列答案
相关题目
下列命题是真命题的是（ ）
| A、a＞b是ac2＞bc2的充要条件 |
| B、a＞1，b＞1是ab＞1的充分条件 |
| C、?x0∈R，e x0≤0 |
| D、若p∨q为真命题，则p∧q为真 |
在Rt△AOB中，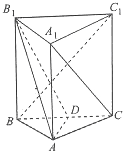
在三棱柱ABC-A1B1C1中，已知平面BB1C1C⊥平面ABC，AB=AC，D是BC中点，且B1D⊥BC1．