题目内容
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审,假设评审结果为“支持”与“不支持”的概率分别为
和
,若某人获得两个“支持”,则给予10万元的创业资助,若只获得一个“支持”,则给予5万元的资助,若未获得“支持”,则不予资助,求:
(1)该公司的资助总额为零的概率
(2)该公司的资助总额超过15万元的概率.
| 2 |
| 3 |
| 1 |
| 3 |
(1)该公司的资助总额为零的概率
(2)该公司的资助总额超过15万元的概率.
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)独立地对每位大学生的创业方案进行评审,该公司的资助总额为零表示三个大学生都没有获得支持,这三个大学生是否获得支持是相互独立的,根据相互独立事件的概率公式得到结果.
(2)公司的资助总额超过15万元,表示三个大学生得到四个支持,五个支持和六个支持,这三个事件之间是互斥的,根据独立重复试验和互斥事件的概率公式得到结果.
(2)公司的资助总额超过15万元,表示三个大学生得到四个支持,五个支持和六个支持,这三个事件之间是互斥的,根据独立重复试验和互斥事件的概率公式得到结果.
解答:
解:(1)由题意知独立地对每位大学生的创业方案进行评审、
∵评审结果为“支持”与“不支持”的概率分别为
和
,
该公司的资助总额为零表示三个大学生都没有获得支持,
这三个大学生是否获得支持是相互独立的,
设A表示资助总额为零这个事件,
则P(A)=(
)6=
,
(2)公司的资助总额超过15万元,表示三个大学生得到四个支持,
五个支持和六个支持,这三个事件之间是互斥的,
设B表示资助总额超过15万元这个事件,
∴P=
(
)4(
)2+
(
)5(
)1+(
)6=
.
∵评审结果为“支持”与“不支持”的概率分别为
| 2 |
| 3 |
| 1 |
| 3 |
该公司的资助总额为零表示三个大学生都没有获得支持,
这三个大学生是否获得支持是相互独立的,
设A表示资助总额为零这个事件,
则P(A)=(
| 1 |
| 3 |
| 1 |
| 729 |
(2)公司的资助总额超过15万元,表示三个大学生得到四个支持,
五个支持和六个支持,这三个事件之间是互斥的,
设B表示资助总额超过15万元这个事件,
∴P=
| C | 4 6 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 5 6 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 496 |
| 729 |
点评:本题考查独立重复试验概率公式,考查互斥事件的概率,考查相互独立事件的概率,是一个综合题,解题的关键是读懂题意.

练习册系列答案
相关题目
等比数列{an}的各项均为正数,且a4a5+a3a6=18,则log3a1+log3a2+…+log3a8=( )
| A、12 | B、10 | C、8 | D、6 |
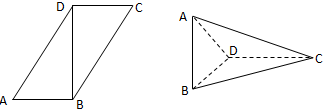
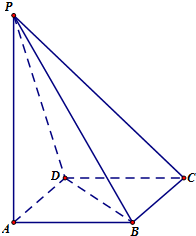 如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,
如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,