题目内容
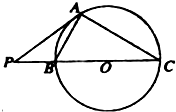如图，已知直线 P A切圆 O于点 A，直线 P O交圆 O于点 B、C，若PC=2+| 3 |
考点：与圆有关的比例线段
专题：立体几何
分析：由切割线定理，得：PA2=PB•PC，从而得到BC=PC-PB=（2+
）-（2-
）=2
，由此能求出圆O的半径长．
| 3 |
| 3 |
| 3 |
解答：
解：∵直线PA切圆O于点A，交圆O与点C，B，
∴由切割线定理，得：PA2=PB•PC，
解得1=PB•（2+
），
∴PB=
=2-
，
∴BC=PC-PB=（2+
）-（2-
）=2
，
∵直线PO过圆心O，∴BC是圆O的直径，
∴圆O的半径长为
．
故答案为：
．
∴由切割线定理，得：PA2=PB•PC，
解得1=PB•（2+
| 3 |
∴PB=
| 1 | ||
2+
|
| 3 |
∴BC=PC-PB=（2+
| 3 |
| 3 |
| 3 |
∵直线PO过圆心O，∴BC是圆O的直径，
∴圆O的半径长为
| 3 |
故答案为：
| 3 |
点评：本题考查圆的半径长的求法，是中档题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
教学练新同步练习系列答案
相关题目
已知函数f（x）在x=x0处可导，则“f′（x0）=0”是“x=x0是f（x）的极值点”的（ ）
| A、充分必要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
总体容量为102，现用系统抽样法抽样，若剔除了2个个体，则抽样间隔可以是（ ）
| A、7 | B、8 | C、9 | D、10 |
已知集合A={x∈Z|-1≤x≤2}，集合B={0，2，4}，则A∩B=（ ）
| A、{0，2} |
| B、{0，2，4} |
| C、{-1，0，2，4} |
| D、{-1，0，1，2，4} |