题目内容
直线x-
y+1=0被圆x2+y2-2x-3=0所截得的弦长为 .
| 3 |
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:由圆的方程求出圆心和半径,求出圆心到直线x-
y+1=0的距离d的值,再根据弦长公式求得弦长.
| 3 |
解答:
解:圆x2+y2-2x-3=0,即(x-1)2+y2=4,表示以C(1,0)为圆心,半径等于2的圆.
由于圆心到直线x-
y+1=0的距离为d=
=1,
故弦长为2
=2
.
故答案为:2
.
由于圆心到直线x-
| 3 |
| 2 | ||
|
故弦长为2
| 4-1 |
| 3 |
故答案为:2
| 3 |
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
相关题目
位于坐标原点的一个支点P按下述规则移动:质点每次移动一个单位:移动的方向为向上或向右,并且向上、向右移动的概率都是0.5,质点P移动6次后位于点(2,4)的概率为( )
A、(
| ||||||
B、C
| ||||||
C、C
| ||||||
D、C
|
若直线y=k(x+4)与曲线x=
有交点,则k的取值范围是( )
| 4-y2 |
A、[-
| ||||||||
B、(-∞,-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
已知a,b是实数,则“lga>lgb”是“(
)a<(
)b”的( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
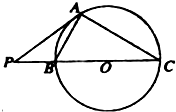 如图,已知直线 P A切圆 O于点 A,直线 P O交圆 O于点 B、C,若PC=2+
如图,已知直线 P A切圆 O于点 A,直线 P O交圆 O于点 B、C,若PC=2+