题目内容
已知函数f（x）在x=x0处可导，则“f′（x0）=0”是“x=x0是f（x）的极值点”的（ ）
| A、充分必要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：导数的概念及应用,简易逻辑
分析：根据可导函数的极值和导数之间的关系，利用充分条件和必要条件的定义即可得到结论．
解答：
解：已知函数f（x）=x3的导数为f'（x）=3x2，由f′（x0）=0，得x0=0，但此时函数f（x）单调递增，无极值，充分性不成立．
根据极值的定义和性质，若x=x0是f（x）的极值点，则f′（x0）=0成立，即必要性成立，
故p是q的必要不充分条件，
故选：B．
根据极值的定义和性质，若x=x0是f（x）的极值点，则f′（x0）=0成立，即必要性成立，
故p是q的必要不充分条件，
故选：B．
点评：本题主要考查充分条件和必要条件的判断，利用函数单调性和极值之间的关系是解决本题的关键，比较基础．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
△ABC中，cosA=
，cosB=-
，则sin（A+B）=（ ）
| 3 |
| 5 |
| 5 |
| 13 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
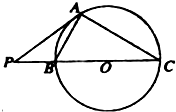如图，已知直线 P A切圆 O于点 A，直线 P O交圆 O于点 B、C，若PC=2+