题目内容
设M=2t+it-1×2t-1+…+i1×2+i0,其中ik=0或1(k=0,1,2,…t-1,t∈N*),并记M(lit-1it-2…i1i0)2.对于给定的x1=(lit-1it-2…i1i0)2,构造无穷数列{xh}如下:x2=(li0it-1it-2…i2i1)2,x3=(li1i0it-1…i3i2)2,x4=(li2i1it-1…i3)2
(1)若x1=27,则x4= (用数字作答);
(2)给定一个正整数m,若x1=22m+2+22m+1+2m+1,则满足xn=x1(n∈N*),且n≠1)的n的最小值为 .
(1)若x1=27,则x4=
(2)给定一个正整数m,若x1=22m+2+22m+1+2m+1,则满足xn=x1(n∈N*),且n≠1)的n的最小值为
考点:数列的应用
专题:新定义,点列、递归数列与数学归纳法
分析:(1)先将x1=27分成24+23+21+1从而得到1it-1it-2…i1i的值,然后根据x4=(li2i1it-1…i3)2进行求解即可;
(2)根据x1=22m+2+22m+1+22m+1则x1=(1i2m+1i2m…i1i)2,从而x2=(1ii2m+1i2m…i1)2,x3=(1i1ii2m+1i2m…i2)2,依此类推x2m+3=x1=(1i2m+1i2m…i1i)2,从而得到结论.
(2)根据x1=22m+2+22m+1+22m+1则x1=(1i2m+1i2m…i1i)2,从而x2=(1ii2m+1i2m…i1)2,x3=(1i1ii2m+1i2m…i2)2,依此类推x2m+3=x1=(1i2m+1i2m…i1i)2,从而得到结论.
解答:
解:(1)∵x1=27=24+23+21+1,
∴x1=24+1×23+0×22+1×2+1,这里i0=1,i1=1,i2=0,i3=1;
∴x4=(1i2i1i0it-1it-2…i4i3)2=2t+i2×2t-1+i1×2t-2+it-1×2t-3+…+i4×2+i3=24+0×23+1×22+1×2+1=23;
(2)∵x1=22m+2+22m+1+22m+1,
∴x1=(1i2m+1i2m…i1i)2而x2=(1ii2m+1i2m…i1)2,x3=(1i1ii2m+1i2m…i2)2,
当i跑到最后时移动了2m+2次,此时x2m+3=x1,
满足xn=x1(n∈N+且n≠1)的n的最小值为2m+3,
故答案为:23;2m+3.
∴x1=24+1×23+0×22+1×2+1,这里i0=1,i1=1,i2=0,i3=1;
∴x4=(1i2i1i0it-1it-2…i4i3)2=2t+i2×2t-1+i1×2t-2+it-1×2t-3+…+i4×2+i3=24+0×23+1×22+1×2+1=23;
(2)∵x1=22m+2+22m+1+22m+1,
∴x1=(1i2m+1i2m…i1i)2而x2=(1ii2m+1i2m…i1)2,x3=(1i1ii2m+1i2m…i2)2,
当i跑到最后时移动了2m+2次,此时x2m+3=x1,
满足xn=x1(n∈N+且n≠1)的n的最小值为2m+3,
故答案为:23;2m+3.
点评:本题考查了数列的综合运用,着重考查二进制的知识应用,解题时,关键是弄清题意,根据新的定义求解,结合所学的知识,细心作答,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有( )
| A、f(0)+f(2)<2f(1) |
| B、f(0)+f(2)≤2f (1) |
| C、f(0)+f(2)≥2f(1) |
| D、f(0)+f(2)>2f (1) |
函数y=xlnx的单调递减区间是( )
| A、(0,e-1) |
| B、(-∞,e-1) |
| C、(e-1,+∞) |
| D、(e,+∞) |
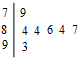 如图是 a,b年在某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是 a,b年在某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、83,1.5 |
| B、84,1.5 |
| C、85,1.6 |
| D、86,1.6 |
