题目内容

观察下表：

设第n行的各数之和为Sn，则
lim
n→∞
Sn
n
2
 
=
 
．
考点：归纳推理,数列的极限
专题：计算题,导数的概念及应用,推理和证明
分析：由题意可归纳出第n项的各数之和Sn=（2n-1）2，从而求
lim
n→∞
Sn
n
2
 
的值．
解答： 解：第一行1=12，
第二行2+3+4=9=32，
第三行3+4+5+6+7=25=52，
第四行4+5+6+7+8+9+10=49=72．
归纳：第n项的各数之和Sn=（2n-1）2，
lim
n→∞
Sn
n
2
 
=
lim
n→∞
（
2n-1
n
）2=4．
故答案为：4．
点评：本题考查了归纳推理的应用及极限的求法，属于中档题．
练习册系列答案
相关题目
在抛物线y=4x2上点P（
 
）到直线y=4x-5的距离最短．
解下列不等式：
（1）|
1
2
x+1|≥2；
（2）|8-x|≤3．
已知二次项系数为正的二次函数f（x）对任意x∈R，都有f（1-x）=f（1+x）成立，设向量
a
=（sinx，2），
b
=（2sinx，
1
2
），
c
=（cos2x，1），
d
=（1，2），当x∈[0，π]时，求不等式f(
a
•
b
)＞f(
c
•
d
)的解集．
设M=2t+it-1×2t-1+…+i1×2+i0，其中ik=0或1（k=0，1，2，…t-1，t∈N*），并记M（lit-1it-2…i1i0）2．对于给定的x1=（lit-1it-2…i1i0）2，构造无穷数列{xh}如下：x2=（li0it-1it-2…i2i1）2，x3=（li1i0it-1…i3i2）2，x4=（li2i1it-1…i3）2
（1）若x1=27，则x4=
 
 （用数字作答）；
（2）给定一个正整数m，若x1=22m+2+22m+1+2m+1，则满足xn=x1（n∈N*），且n≠1）的n的最小值为
 
．
若椭圆2kx2+ky2=1的一个焦点坐标是（0，4），则k的值为（　　）
A、
1
8
B、
1
32
C、2
D、
3
16
随着我国加入WTO，某企业决定从甲、乙两种产品中选择一种投资生产，打入国际市场，已知投资生产这两种产品的有关数据如表：（单位：万元）
年固定成品每件产品成本每件产品销售价每件可最多生产件数
甲产品20a10200
乙产品40818120
其中年固定成本与年生产的件数无关，a为常数，且3≤a≤8．另外，年销售x件乙产品时需上交0.05x2万美元的特别关税．
（Ⅰ）写出该厂分别投资生产甲、乙两产品的年利润y1，y2与生产相应产品的件数x（x∈N）之间的函数关系；
（Ⅱ）分别求出投资生产这两种产品的最大年利润；
（Ⅲ）如何决定投资可获最大年利润．
已知曲线C：y=x3-3x2+2x，直线l：y=kx，且l与C切于点（x0，y0）（x0≠0），则切点坐标是
 
．
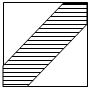在边长为25cm的正方形中挖去腰长为23cm的两个等腰直角三角形（如图），现有均匀的粒子散落在正方形中，问粒子落在中间带形区域的概率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网