题目内容
设F1,F2分别为椭圆C:
+
=1(a>b>0)的左、右两个焦点;
①若椭圆C上的点A(1,
)到F1,F2两点的距离之和等于4,写出椭圆C的方程;
②设K是①中所得椭圆上的动点,求线段F1K的中点的轨迹方程.
| x2 |
| a2 |
| y2 |
| b2 |
①若椭圆C上的点A(1,
| 3 |
| 2 |
②设K是①中所得椭圆上的动点,求线段F1K的中点的轨迹方程.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:对第①问,由题干条件及椭圆定义,得a,将点A的坐标代入椭圆方程中,得b2,从而得椭圆的方程;
对第②问,设动点K(x0,y0),设F1K的中点为M(x,y),用x,y分别表示x0,y0,再将坐标(x0,y0)代入椭圆方程中,即得动点M的轨迹方程.
对第②问,设动点K(x0,y0),设F1K的中点为M(x,y),用x,y分别表示x0,y0,再将坐标(x0,y0)代入椭圆方程中,即得动点M的轨迹方程.
解答:
解:①由椭圆的定义知,|AF1|+|AF2|=2a,即4=2a,得a2=4,
从而椭圆C的方程可写成
+
=1.
将A的坐标(1,
)代入上式中,得
+
=1,得b2=3,
所以椭圆C的方程为
+
=1.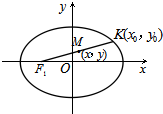
②由①知,F1的坐标为(-1,0),设动点K(x0,y0),线段F1K的中点为M(x,y),如右图所示.
则由中点公式,有
,变形为
,
将上式代入
+
=1中,得
+
=1,
即得线段F1K中点的轨迹方程为(x+
)2+
=1.
从而椭圆C的方程可写成
| x2 |
| 4 |
| y2 |
| b2 |
将A的坐标(1,
| 3 |
| 2 |
| 12 |
| 4 |
(
| ||
| b2 |
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |

②由①知,F1的坐标为(-1,0),设动点K(x0,y0),线段F1K的中点为M(x,y),如右图所示.
则由中点公式,有
|
|
将上式代入
| ||
| 4 |
| ||
| 3 |
| (2x+1)2 |
| 4 |
| (2y)2 |
| 3 |
即得线段F1K中点的轨迹方程为(x+
| 1 |
| 2 |
| y2 | ||
|
点评:本题考查了椭圆的方程,椭圆的定义,轨迹方程的求法,利用相关点法求轨迹方程的一般步骤是:
(1)设轨迹上的点为M(x,y),其他点(即相关点)设为(x0,y0),(x1,y1),(x2,y2)等;
(2)寻找x,y与相关点的关系,用x,y表示相关点;
(3)将相关点的坐标代入曲线方程中,化简,整理,即得动点M的轨迹方程.
(1)设轨迹上的点为M(x,y),其他点(即相关点)设为(x0,y0),(x1,y1),(x2,y2)等;
(2)寻找x,y与相关点的关系,用x,y表示相关点;
(3)将相关点的坐标代入曲线方程中,化简,整理,即得动点M的轨迹方程.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=
,A+C=2B,则sinC=( )
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
设z=1-i复数,则复数1+z2在复平面内所对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
同时掷两枚硬币,那么互为对立事件的是( )
| A、至少有1枚正面和恰好有1枚正面 |
| B、恰好有1枚正面和恰好有2枚正面 |
| C、最多有1枚正面和至少有2枚正面 |
| D、至少有2枚正面和恰好有1枚正面 |
椭圆
+
=1的两焦点F1,F2,过F2引直线L交椭圆于A、B两点,则△ABF1的周长为( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、5 | B、15 | C、10 | D、20 |