题目内容

在三棱锥P-ABC中，PA、PB、PC两两互相垂直，且PA=PB=PC=2，则三棱锥P-ABC的外接球的球面面积是
 
．
考点：球的体积和表面积
专题：计算题,高考数学专题
分析：以PA、PB、PC为过同一顶点的三条棱，作长方体如图，则长方体的外接球同时也是三棱锥P-ABC外接球．算出长方体的对角线即为球直径，结合球的表面积公式，可算出三棱锥P-ABC外接球的表面积．
解答： 解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图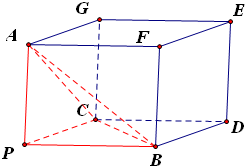
则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为2
3
，
∴球直径为2
3
，半径R=
3
，
因此，三棱锥P-ABC外接球的表面积是4πR2=4π×（
3
）2=12π
故答案为：12π．
点评：本题给出三棱锥的三条侧棱两两垂直，求它的外接球的表面积，着重考查了长方体对角线公式和球的表面积计算等知识，属于基础题．
练习册系列答案
相关题目
设z=1-i复数，则复数1+z2在复平面内所对应的点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
椭圆
x2
25
+
y2
9
=1的两焦点F1，F2，过F2引直线L交椭圆于A、B两点，则△ABF1的周长为（　　）
A、5B、15C、10D、20
由曲线y2=2x与直线y=-x+4所围成的封闭图形的面积为
 
．
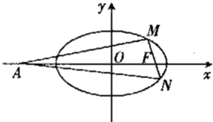如图所示，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
6
3
，F为椭圆在x轴正半轴上的焦点，M、N两点在椭圆C上，且
MF
=λ
FN
（λ＞0），定点A（-4，0），当λ=1时，有
AM
•
AN
=
106
3
．
（Ⅰ）求椭圆C的方程．
（Ⅱ）当M、N两点在椭圆C上运动时，试判断
AM
•
AN
•tan∠MAN是否有最大值，若存在，求出最大值，并求出这时M、N两点所在直线方程，若不存在，请说明理由．
解下列不等式：
（1）|
1
2
x+1|≥2；
（2）|8-x|≤3．
定义：a*b=
a(a-b≤0)
b(a-b＞0)
，当正数p取何值时，关于x的方程：
1
p
[（2x2-4x+2）*（x+2）]-2=0有三个不同的实数解？有两个不同实数解？有唯一实数解？分别求出p的取值范围．
设M=2t+it-1×2t-1+…+i1×2+i0，其中ik=0或1（k=0，1，2，…t-1，t∈N*），并记M（lit-1it-2…i1i0）2．对于给定的x1=（lit-1it-2…i1i0）2，构造无穷数列{xh}如下：x2=（li0it-1it-2…i2i1）2，x3=（li1i0it-1…i3i2）2，x4=（li2i1it-1…i3）2
（1）若x1=27，则x4=
 
 （用数字作答）；
（2）给定一个正整数m，若x1=22m+2+22m+1+2m+1，则满足xn=x1（n∈N*），且n≠1）的n的最小值为
 
．
已知平面向量向量
a
=（
3
，-1），向量
b
=（
1
2
，
3
2
）．
（1）求证：
a
⊥
b
；
（2）令
m
=
a
+（sin2α-2cosα）
b
，
n
=（
1
4
sin22α）
a
+（cosα）
b
，若
m
⊥
n
，α∈（0，π），求角α．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网