题目内容
12.已知函数f(x)=$\frac{1}{3}{x^3}-{x^2}$+ax在x=-1是取得极值.(1)求实数a的值;
(2)求函数y=f(x)在区间[-2,0)上的最大值和最小值.
分析 (1)求出函数的导数,根据f′(-1)=0,求出a的值即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可.
解答 解:(1)f′(x)=x2-2x+a,
由函数在x=-1处取极值,故f′(-1)=0,
即1+2+a=0,解得:a=-3;
(2)由(1)得:f(x)=$\frac{1}{3}$x3-x2-3x,
故f′(x)=x2-2x-3=(x-3)(x+1),
令f′(x)>0,解得:x>3或x<-1,
令f′(x)<0,解得:-1<x<3,
故f(x)在[-2,-1)递增,在(-1,0)递减,
由f(-2)=-$\frac{2}{3}$,f(-1)=$\frac{5}{3}$,
故f(x)max=f(-1)=$\frac{5}{3}$,
f(x)min=f(-2)=-$\frac{2}{3}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及极值的意义,是一道中档题.

练习册系列答案
相关题目
2.已知集合A={x|x+2>0},B={x|x2+2x-3≤0},则A∩B=( )
| A. | [-3,-2) | B. | [-3,-1] | C. | (-2,1] | D. | [-2,1] |
20.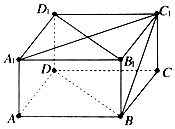 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值等于( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{10}$ |
17.若sin(θ+3π)=$\frac{4}{5}$,tan(θ-π)>0,则cosθ=( )
| A. | $\frac{3}{5}$ | B. | $-\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.下列函数中,既是奇函数又是增函数的是( )
| A. | y=x|x| | B. | y=-x3 | C. | y=$\frac{1}{x}$ | D. | y=sinx |
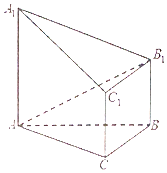 如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.
如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.