题目内容
1.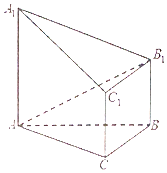 如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.
如图,已知AA1⊥平面ABC,BB1∥CC1∥AA1,$AC=\sqrt{3}$,$BC=\sqrt{2}$,AA1=2BB1=2CC1=2,BC⊥AC.(1)求证:B1C1⊥平面A1ACC1;
(2)求直线AB1与平面A1B1C1所成的角.
分析 (1)证明BC⊥平面A1ACC1,BC∥B1C1,即可证明:B1C1⊥平面A1ACC1;
(2)取A1C1中点D,连AD,连接B1D,可得∠AB1D是直线AB1与平面A1B1C1所成的角,即可求直线AB1与平面A1B1C1所成的角.
解答 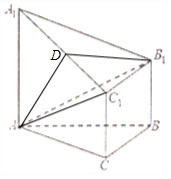 (1)证明:∵AA1⊥平面ABC,BC?平面ABC,∴BC⊥AA1…(2分)
(1)证明:∵AA1⊥平面ABC,BC?平面ABC,∴BC⊥AA1…(2分)
∵BC⊥AC,AA1,AC是平面A1ACC1内的两条相交直线 …(4分)
∴BC⊥平面A1ACC1
∵BB1∥CC1,且BB1=CC1=1,∴四边形C1CBB1是平行四边形
∴BC∥B1C1…(5分)
∴B1C1⊥平面A1ACC1…(6分)
(2)解:连接AC1,在直角△ACC1中,AC1=2,在直角梯形A1ACC1中,A1C1=2
∴△AA1C1是边长为2的正三角形,取A1C1中点D,连AD,则AD⊥A1C1且$AD=\sqrt{3}$…(7分)
∵B1C1⊥平面A1ACC1,AD?平面A1ACC1,∴AD⊥B1C1
∵A1C1∩B1C1=C1,
∴AD⊥平面A1B1C1,
连接B1D,∴∠AB1D是直线AB1与平面A1B1C1所成的角.
在直角△ABC中,AB=$\sqrt{5}$,又AB1=$\sqrt{6}$,
∴在直角△AB1D中,$sin∠A{B_1}D=\frac{AD}{{A{B_1}}}=\frac{{\sqrt{3}}}{{\sqrt{6}}}=\frac{{\sqrt{2}}}{2}$,∴∠AB1D=45°…(12分)
点评 本题考查线面垂直的判定,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.若复数(a2+i)(1+ai)(a∈R)是实数,则实数a的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
9.将函数y=sin2x的图象向左平移φ(φ>0)个单位,得到的图象恰好关于直线x=$\frac{π}{6}$对称,则φ的最小值是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
16.命题:“存在一个椭圆,其离心率e<1”的否定是( )
| A. | 任意椭圆的离心率e≥1 | B. | 存在一个椭圆,其离心率e≥1 | ||
| C. | 任意椭圆的离心率e>1 | D. | 存在一个椭圆,其离心率e>1 |
7.已知圆(x-1)2+y2=$\frac{3}{4}$的一条切线y=kx与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有两个交点,则双曲线C的离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | (1,2) | C. | ($\sqrt{3}$,+∞) | D. | (2,+∞) |
4.已知M、N是焦点为F的抛物线y2=4x上两个不同点,且线段MN的中点A的横坐标是3,直线MN与x轴交于点B,则点B的横坐标的取值范围是( )
| A. | (-3,3] | B. | (-∞,3] | C. | (-6,-3] | D. | (-6,3) |