下列事件:①抛一枚硬币.出现正面朝上,②某人买彩票中奖,③大年初一太原下雪,④标准大气压下.水加热到90°C时会沸腾．其中随机事件的个数是( )A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

7．下列事件：①抛一枚硬币，出现正面朝上；②某人买彩票中奖；③大年初一太原下雪；④标准大气压下，水加热到90°C时会沸腾．其中随机事件的个数是（　　）

A．

B．

C．

D．

分析依据随机事件定义，即随机事件就是可能发生也可能不发生的事件，即可判断出事件中是随机事件的个数．

解答解：依据随机事件定义，可知①②③是随机事件，
故选C．

点评解决本题需要正确理解必然事件、不可能事件、随机事件的概念．用到的知识点为：必然事件指在一定条件下一定发生的事件；不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．

练习册系列答案

18．如图1，ABCD为长方形，AB=3，AD=$\sqrt{2}$，E，F分别是边AB，CD上的点，且AE=CF=1，DE与AF相交于点G，将三角形ADF沿AF折起至ADF'，使得D'E=1，如图2．
（1）求证：平面D'EG⊥ABCF平面；
（2）求平面D'EG与平面所成锐二面角的余弦值．

15．已知点P是双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）右支上一点，F₁，F₂分别是双曲线的左、右焦点，I为△PF₁F₂的内心，若S${\;}_{△IP{F}_{1}}$=S${\;}_{△IP{F}_{2}}$$+\frac{1}{2}$S${\;}_{△I{F}_{1}{F}_{2}}$成立，则双曲线的离心率为（　　）

2．已知集合A={x|0＜2x+a≤3}，B={x|-$\frac{1}{2}$＜x＜2}．
（1）当a=1时，求（∁_RB）∪A；
（2）若A⊆B，求实数a的取值范围．

12．已知函数f（x）=$\frac{1}{3}{x^3}-{x^2}$+ax在x=-1是取得极值．
（1）求实数a的值；
（2）求函数y=f（x）在区间[-2，0）上的最大值和最小值．

19．设a=log₃7，b=2^1.1，c=0.5^2.1，则（　　）

16．命题：“存在一个椭圆，其离心率e＜1”的否定是（　　）

	A．	任意椭圆的离心率e≥1		B．	存在一个椭圆，其离心率e≥1
	C．	任意椭圆的离心率e＞1		D．	存在一个椭圆，其离心率e＞1

11．

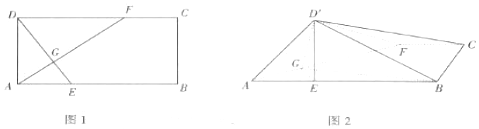
如图，已知长方体ABCD-A₁B₁C₁D₁的体积为6，∠C₁BC的正切值为$\frac{1}{3}$，当AB+AD+AA₁的值最小时，长方体ABCD-A₁B₁C₁D₁外接球的表面积（　　）

试题分类