题目内容
设双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为e,过F2的直线与双曲线的右支交于A,B两点,若△F1AB是以A为直角顶点的等腰直角三角形,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、1+2
| ||
B、4-2
| ||
C、5-2
| ||
D、3+2
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用双曲线的定义等腰直角三角形的性质可得|AF1|-|AF2|=2a,|BF1|-|BF2|=2a,|BF1|=|AF2|+|BF2|,再利用等腰直角三角形的性质、勾股定理即可得出.
解答:
解:如图所示,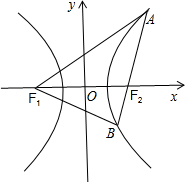
∵|AF1|-|AF2|=2a,|BF1|-|BF2|=2a,
|BF1|=|AF2|+|BF2|,
∴|AF2|=2a,|AF1|=4a.
∴|BF1|=2
a,
∴|BF2|=2
a-2a.
∵|F1F2|2=|BF1|2+|BF2|2,
∴(2c)2=(2
a)2+(2
a-2a)2,
∴e2=5-2
.
故选:C.

∵|AF1|-|AF2|=2a,|BF1|-|BF2|=2a,
|BF1|=|AF2|+|BF2|,
∴|AF2|=2a,|AF1|=4a.
∴|BF1|=2
| 2 |
∴|BF2|=2
| 2 |
∵|F1F2|2=|BF1|2+|BF2|2,
∴(2c)2=(2
| 2 |
| 2 |
∴e2=5-2
| 2 |
故选:C.
点评:本题考查了双曲线的定义等腰直角三角形的性质、勾股定理,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
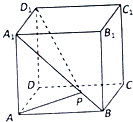 如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )
如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
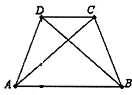 在等腰梯形ABCD中,AB∥CD,且AB>CD.设以A,B为焦点且过点D的双曲线的离心率为2,以C,D为焦点且过点A的椭圆的离心率e等于( )
在等腰梯形ABCD中,AB∥CD,且AB>CD.设以A,B为焦点且过点D的双曲线的离心率为2,以C,D为焦点且过点A的椭圆的离心率e等于( )