题目内容
天津高考数学试卷共有8道选择题,在每小题给出的四个选项中,只有一项是符合题目要求的,评分标准规定:“选对得5分,不选或选错得0分”.某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(Ⅰ)该考生得40分的概率;
(Ⅱ)写出该考生所得分数孝的分布列,并求:
①该考生得多少分的可能性最大?
②该考生所得分数ξ的数学期望•
(Ⅰ)该考生得40分的概率;
(Ⅱ)写出该考生所得分数孝的分布列,并求:
①该考生得多少分的可能性最大?
②该考生所得分数ξ的数学期望•
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)设选对一道“可判断2个选项是错误的”题目为事件A,“可判断1个选项是错误的”该题选对为事件B,“不能理解题意的”该题选对为事件C,则P(A)=
,P(B)=
,P(C)=
,由此能求出该考生得40分的概率.
(Ⅱ)①该考生所得分数ξ=20,25,30,35,40,分别求出相应的概率,由此能求出该考生得25分或30分的可能性最大.
②由①能求出Eξ.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅱ)①该考生所得分数ξ=20,25,30,35,40,分别求出相应的概率,由此能求出该考生得25分或30分的可能性最大.
②由①能求出Eξ.
解答:
解:(Ⅰ)设选对一道“可判断2个选项是错误的”题目为事件A,
“可判断1个选项是错误的”该题选对为事件B,
“不能理解题意的”该题选对为事件C,
则P(A)=
,P(B)=
,P(C)=
,
∴该考生得40分的概率:
P=[P(A)]2•P(B)•P(C)=
×
×
=
.
(Ⅱ)①该考生所得分数ξ=20,25,30,35,40,
P(ξ=20)=[P(
)]2P(
)P(
)=
×
×
=
,
P(ξ=25)=
P(A)P(
)P(
)P(
)+[P(
)]2P(B)P(
)+[P(
)]2P(
)P(
)
=2×(
)2×
×
+
×
×
+
×
×
=
,
P(ξ=30)=[P(A)]2P(
)P(
)+
P(
)P(A)P(
)P(C)+[P(
)]2P(B)P(C)
=(
)2×
×
+2×
×
×
×
+2×
×
×
×
+(
)2×
×
=
,
P(ξ=35)=
P(A)P(
)P(B)P(C)+[P(A)]2P(
)P(
)
=2×
×
×
×
+(
)2×
×
+(
)2×
×
=
,
P(ξ=40)=1-
-
-
-
=
,
∴该考生得25分或30分的可能性最大.
②Eξ=20×
+25×
+30×
+35×
+40×
=
.
“可判断1个选项是错误的”该题选对为事件B,
“不能理解题意的”该题选对为事件C,
则P(A)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
∴该考生得40分的概率:
P=[P(A)]2•P(B)•P(C)=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 48 |
(Ⅱ)①该考生所得分数ξ=20,25,30,35,40,
P(ξ=20)=[P(
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 6 |
| 48 |
P(ξ=25)=
| C | 1 2 |
. |
| A |
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
. |
| C |
=2×(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 17 |
| 48 |
P(ξ=30)=[P(A)]2P(
. |
| B |
. |
| C |
| C | 1 2 |
. |
| A |
. |
| B |
. |
| A |
=(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 17 |
| 48 |
P(ξ=35)=
| C | 1 2 |
. |
| A |
. |
| B |
. |
| C |
=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 7 |
| 48 |
P(ξ=40)=1-
| 6 |
| 48 |
| 17 |
| 48 |
| 17 |
| 48 |
| 7 |
| 48 |
| 1 |
| 48 |
∴该考生得25分或30分的可能性最大.
②Eξ=20×
| 6 |
| 48 |
| 17 |
| 48 |
| 17 |
| 48 |
| 7 |
| 48 |
| 1 |
| 48 |
| 335 |
| 12 |
点评:本题考查概率的求法,考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
以抛物线y=
x2的焦点为圆心,3为半径的圆与直线4x+3y+2=0相交所得的弦的长度是( )
| 1 |
| 4 |
A、
| ||||
B、4
| ||||
C、2
| ||||
| D、8 |
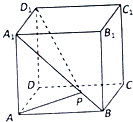 如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )
如图所示,在棱长为l的正方体ABCD-ABCD的面对角线AB上存在一点P使得AP+DP取得最小值,则此最小值为( )| A、2 | ||||||
B、
| ||||||
C、2+
| ||||||
D、
|
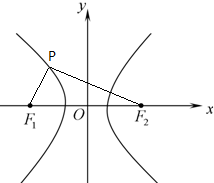 如图,若F1,F2是双曲线
如图,若F1,F2是双曲线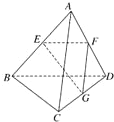 如图,已知空间四边形ABCD的每条边及AC、BD的长都为a,点E、F、G分别是AB、AD、DC的中点,求:
如图,已知空间四边形ABCD的每条边及AC、BD的长都为a,点E、F、G分别是AB、AD、DC的中点,求: