题目内容
已知
=(1,2),
=(3,n),若
∥
,则n等于( )
| AB |
| CD |
| AB |
| CD |
| A、3 | B、4 | C、5 | D、6 |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:利用向量平行的坐标运算得到n的关系式,求出n即可.
解答:
解:
=(1,2),
=(3,n),
∵
∥
,
∴1•n=2×3,
∴n=6.
故选:D.
| AB |
| CD |
∵
| AB |
| CD |
∴1•n=2×3,
∴n=6.
故选:D.
点评:本题考查向量共线与向量的平行的坐标运算,考查计算能力.

练习册系列答案
相关题目
若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则a的取值范围是( )
| A、(-∞,0]∪[1,+∞) |
| B、(-1,0) |
| C、[-1,0] |
| D、(-∞,-1]∪[0,+∞) |
等比数列{an}中,a3=16,a4=8,则a1=( )
| A、64 | B、32 | C、4 | D、2 |
已知i是虚数单位,设复数z1=1-i,z2=1-2i,则z1•z2在复平面内对应点的坐标是( )
| A、(1,3) |
| B、(-1,3) |
| C、(-1,-3) |
| D、(3,-3) |
集合A={x|x2>1},B={x|x+a≥0},若∁UA⊆B,则实数a的取值范围是( )
| A、[-1,+∞) |
| B、[1,+∞) |
| C、(-∞,1] |
| D、(-∞,-1] |
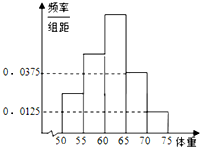 为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是
为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是 某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )
某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )