题目内容
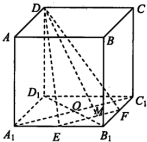 如图,在正方形ABCD=A1B1C1D1中,AB=2,O为底面正方形A1B1C1D1的中心,E、F分别为A1B1、B1C1的中点,点M为EF上一点,且满足
如图,在正方形ABCD=A1B1C1D1中,AB=2,O为底面正方形A1B1C1D1的中心,E、F分别为A1B1、B1C1的中点,点M为EF上一点,且满足| EM |
| 2 |
| 3 |
| EF |
(Ⅰ)求证:平面DEF⊥平面BB1DD1.
(Ⅱ)若OP与DM相交,试判断OM与DP的位置关系;
(Ⅲ)在(Ⅱ)的条件下,求平面CDP与平面DPO所成锐二面角的大小为θ,求cosθ
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)利用线面垂直证明面面垂直,EF⊥面BB1D1D,面DEF⊥面BB1D1;(Ⅱ)先证OM与DP共面,在利用正方体的几何性质证明DP∥OM;(Ⅲ)建立空间坐标系,用向量法解决.
解答:
本题满分(13分).
(Ⅰ)证明:在正方体ABCD-A1B1C1D1中,
∵A1C1⊥B1D1,BB1⊥A1C1…(1分)
∵E,F分别为A1B1,B1C1的中点,∴EF∥A1C1…(2分)∴EF⊥B1D1,EF⊥BB1,B1D1∩BB1=B1,∴EF⊥面BB1D1D
又EF?面DEF…(3分)∴面DEF⊥面BB1D1D…(4分)
(Ⅱ)∵OP与DM相交,
∴OP与DM确定一个平面α,P为正方体底面ABCD上的点…(5分)
∴平面α∩面ABCD=DP,平面α∩面A1B1C1D1=OM…(6分)
∵在正方体ABCD-A1B1C1D1中,面ABCD∥面A1B1C1D1∴DP∥OM…(7分)
(Ⅲ)如图以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,
y轴,z轴建立空间直角坐标系,则A1(2,0,0),B1(2,2,0),C1(0,2,0),O(1,1,0),D(0,0,2),E(2,1,0),F(1,2,0)…(8分)
设M(m,n,0),
由
=
,得(m-2,n-1,0)=
(-1,1,0)
解得m=
,n=
,即M(
,
,0)…(10分)
由(Ⅱ)可知:面CPD与面ABCD共面,
面DOP与面DOM共面,
面ABCD的一个法向量为
=(0, 0, 1)
设面DOM的一个法向量为
=(x,y,z),∵
=(-1, -1, 2),
=(
,
, 0)
∴由
,可得
令z=1,则x=4,y=-2,即
=(4, -2, 1)…(12分)
cos?
,
>=
=
,故cosθ=
…(13分)
(Ⅰ)证明:在正方体ABCD-A1B1C1D1中,
∵A1C1⊥B1D1,BB1⊥A1C1…(1分)
∵E,F分别为A1B1,B1C1的中点,∴EF∥A1C1…(2分)∴EF⊥B1D1,EF⊥BB1,B1D1∩BB1=B1,∴EF⊥面BB1D1D
又EF?面DEF…(3分)∴面DEF⊥面BB1D1D…(4分)
(Ⅱ)∵OP与DM相交,
∴OP与DM确定一个平面α,P为正方体底面ABCD上的点…(5分)
∴平面α∩面ABCD=DP,平面α∩面A1B1C1D1=OM…(6分)
∵在正方体ABCD-A1B1C1D1中,面ABCD∥面A1B1C1D1∴DP∥OM…(7分)
(Ⅲ)如图以D1为原点,D1A1,D1C1,D1D所在直线分别为x轴,
y轴,z轴建立空间直角坐标系,则A1(2,0,0),B1(2,2,0),C1(0,2,0),O(1,1,0),D(0,0,2),E(2,1,0),F(1,2,0)…(8分)
设M(m,n,0),
由
| EM |
| 2 |
| 3 |
| EF |
| 2 |
| 3 |
解得m=
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
由(Ⅱ)可知:面CPD与面ABCD共面,
面DOP与面DOM共面,
面ABCD的一个法向量为
| n1 |
设面DOM的一个法向量为
| n2 |
| OD |
| OM |
| 1 |
| 3 |
| 2 |
| 3 |
∴由
|
|
令z=1,则x=4,y=-2,即
| n2 |
cos?
| n1 |
| n2 |
| 1 | ||
1×
|
| ||
| 21 |
| ||
| 21 |
点评:本题考查面面垂直,空间直线的位置关系,二面角的平面角,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
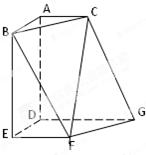 如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4.
如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.