题目内容
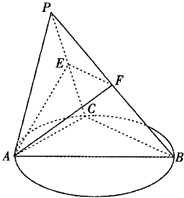 如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.(Ⅰ)求证:直线l⊥平面PAC;
(Ⅱ)直线l上是否存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余?若存在,求出|AQ|的值;若不存在,请说明理由.
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)利用三角形中位线定理推导出BC∥面EFA,从而得到BC∥l,再由已知条件推导出BC⊥面PAC,由此证明l⊥面PAC.
(2)以C为坐标原点,CA为x轴,CB为y轴,过C垂直于面ABC的直线为z轴,建立空间直角坐标系,利用向量法求出直线l上存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余,|AQ|=1.
(2)以C为坐标原点,CA为x轴,CB为y轴,过C垂直于面ABC的直线为z轴,建立空间直角坐标系,利用向量法求出直线l上存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余,|AQ|=1.
解答:
(Ⅰ)证明:∵E,F分别是PB,PC的中点,∴BC∥EF,
又EF?平面EFA,BC不包含于平面EFA,
∴BC∥面EFA,
又BC?面ABC,面EFA∩面ABC=l,
∴BC∥l,
又BC⊥AC,面PAC∩面ABC=AC,
面PAC⊥面ABC,∴BC⊥面PAC,
∴l⊥面PAC.
(2)解:以C为坐标原点,CA为x轴,CB为y轴,
过C垂直于面ABC的直线为z轴,建立空间直角坐标系,
A(2,0,0),B(0,4,0),P(1,0,
),
E(
,0,
),F(
,2,
),
=(-
,0,
),
=(0,2,0),
设Q(2,y,0),面AEF的法向量为
=(x,y,z),
则
,
取z=
,得
=(1,0,
),
=(1,y,-
),
|cos<
,
>|=|
|=
,
|cos<
,
>|=|
|=
,
依题意,得|cos<
,
>|=|cos<
,
>|,
∴y=±1.
∴直线l上存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余,|AQ|=1.
又EF?平面EFA,BC不包含于平面EFA,
∴BC∥面EFA,

又BC?面ABC,面EFA∩面ABC=l,
∴BC∥l,
又BC⊥AC,面PAC∩面ABC=AC,
面PAC⊥面ABC,∴BC⊥面PAC,
∴l⊥面PAC.
(2)解:以C为坐标原点,CA为x轴,CB为y轴,
过C垂直于面ABC的直线为z轴,建立空间直角坐标系,
A(2,0,0),B(0,4,0),P(1,0,
| 3 |
E(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AE |
| 3 |
| 2 |
| ||
| 2 |
| EF |
设Q(2,y,0),面AEF的法向量为
| m |
则
|
取z=
| 3 |
| m |
| 3 |
| PQ |
| 3 |
|cos<
| PQ |
| EF |
| 2y | ||
2
|
| |y| | ||
|
|cos<
| PQ |
| m |
| 1-3 | ||
2
|
| 1 | ||
|
依题意,得|cos<
| PQ |
| EF |
| PQ |
| m |
∴y=±1.
∴直线l上存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余,|AQ|=1.
点评:本题考查直线与平面垂直的证明,考查满足条件的点是否存在的判断与求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上. 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.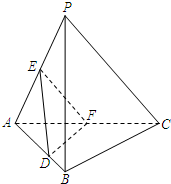 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证: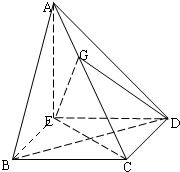 如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6
如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6