题目内容
已知函数y=ax2-4x-1在﹙2，+∞﹚上是增函数，求实数a的取值范围．
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据函数单调性的性质建立条件关系即可得到结论．
解答：
解：若a=0，则函数为y=-4x-1在R上是减函数，不满足条件．
若a≠0，要使函数y=ax2-4x-1在﹙2，+∞﹚上是增函数，
则
，
则
，即a≥1．
故实数a的取值范围是a≥1．
若a≠0，要使函数y=ax2-4x-1在﹙2，+∞﹚上是增函数，
则
|
则
|
故实数a的取值范围是a≥1．
点评：本题主要考查函数单调性的应用，注意要对a进行分类讨论．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知方程
+
=1表示椭圆，则k的取值范围为（ ）
| x2 |
| 3+k |
| y2 |
| 2-k |
| A、k＜2 | B、k＞-3 |
| C、-3＜k＜2 | D、以上都不对 |
已知命题“若p，则q”是真命题，对下列命题中一定是真命题的是（ ）
| A、若q，则p |
| B、￢p，则￢q |
| C、若￢q，则￢p |
| D、若￢p，则q |
直三棱柱ABC-A1B1C1中，AB⊥AC，AC=AA1，AC1与A1C交于一点P，延长B1B到D，使得BD=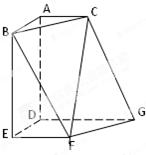
如图，在多面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，BA⊥AC，ED⊥DG，EF∥DG且AC=1，AB=ED=EF=2，AD=DG=4．
某装修公司根据客户要求装饰一个墙角，施工设计时，在墙面交线AB与天花板ACD之间拉一条“定位线”EF（如图），已知墙面交线AB、AC、AD两两垂直，且AB=2，AC=AD=3．（单位：分米）