题目内容
已知a，b，c∈R，a2+2b2+3c2=6，求a+b+c的最大值．
考点：二维形式的柯西不等式
专题：计算题,不等式
分析：考虑到柯西不等式（a2+b2+c2）（x2+y2+z2）≥（ax+by+cz）2的应用，构造出柯西不等式求出（a+b+c）2的最大值开方即可得到答案．
解答：
解：因为已知a、b、c是实数，且a2+2b2+3c2=6，
根据柯西不等式（a2+b2+c2）（x2+y2+z2）≥（ax+by+cz）2
故有（a2+2b2+3c2）（1+
+
）≥（a+b+c）2
故（a+b+c）2≤11，即a+b+c的最大值为
，当且仅当a=2b=3c=
时，等号成立．
根据柯西不等式（a2+b2+c2）（x2+y2+z2）≥（ax+by+cz）2
故有（a2+2b2+3c2）（1+
| 1 |
| 2 |
| 1 |
| 3 |
故（a+b+c）2≤11，即a+b+c的最大值为
| 11 |
6
| ||
| 11 |
点评：此题主要考查一般形式的柯西不等式的应用，对于此类题目很多同学一开始就想到应用参数方程求解，这个方法可行但是计算量较高，而应用柯西不等式求解较简单，同学们需要很好的理解掌握．
练习册系列答案
相关题目
某装修公司根据客户要求装饰一个墙角，施工设计时，在墙面交线AB与天花板ACD之间拉一条“定位线”EF（如图），已知墙面交线AB、AC、AD两两垂直，且AB=2，AC=AD=3．（单位：分米）
如图，已知AB是圆柱OO1底面圆O的直径，底面半径R=1，圆柱的表面积为8π；点C在底面圆O上，且直线A1C与下底面所成的角的大小为60°．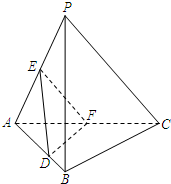
如图，在三棱锥P-ABC中，平面PAC⊥平面ABC，∠BAC=60°，E，F分别是AP，AC的中点，点D在棱AB上，且AD=AC．求证：