题目内容
15.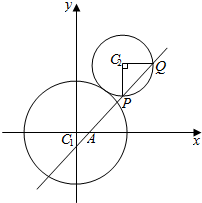 已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.
已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.(1)若圆C2关于直线l:$\frac{ax}{9}$-$\frac{by}{12}$=1对称,求由点M(a,b)向圆C2所作的切线长的最小值;
(2)若直线l1过点A(1,0),与圆C2相交于P、Q两点.且S${\;}_{△{C}_{2}PQ}$=2求此时直线l1的方程.
分析 (1)先求出r=2,a-b=3,再求由点M(a,b)向圆C2所作的切线长的最小值;
(2)求出圆心到直线的距离为$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,即可求此时直线l1的方程.
解答 解:∵圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切,
∴5=3+r,∴r=2.
∵圆C2关于直线l:$\frac{ax}{9}$-$\frac{by}{12}$=1对称,
∴a-b=3,
由点M(a,b)向圆C2所作的切线长=$\sqrt{(a-3)^{3}+(b-4)^{2}-4}$=$\sqrt{2(b-2)^{2}+4}$,
∴b=2时,由点M(a,b)向圆C2所作的切线长的最小值为2;
(2)∵S${\;}_{△{C}_{2}PQ}$=2,
∴C2P⊥C2Q,
∴圆心到直线的距离为$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
设直线l的方程为y=k(x-1),即kx-y-k=0,
∴$\frac{|2k-4|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,
∴k=1或7,
∴直线l的方程为x-y-1=0或7x-y-7=0.
点评 本题考查直线与圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知数列{an}中,a1=1,(n+1)an+1=2(a1+a2+…+an)(n∈N+),则数列{an}的通项公式是( )
| A. | an=$\frac{n+1}{3}$ | B. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+2}{4},n≥2}\end{array}\right.$ | ||
| C. | an=$\frac{n+1}{2}$ | D. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$ |
5.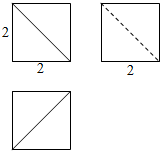 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{20}{3}$ | B. | 18 | C. | $24+2\sqrt{3}$ | D. | $18+2\sqrt{3}$ |
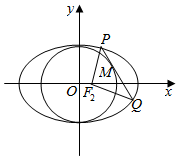 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上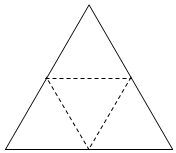 如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.
如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.