题目内容
14.当x>0时,证明不等式1n(1+x)>x-$\frac{1}{2}$x2成立.分析 令f(x)=ln(1+x)+$\frac{1}{2}$x2-x,(x>0),求出函数的导数,得到函数的单调区间,从而证出结论.
解答 证明:令f(x)=ln(1+x)+$\frac{1}{2}$x2-x,(x>0),
则f′(x)=$\frac{1}{x+1}$+x-1=$\frac{{x}^{2}}{x+1}$>0,
∴f(x)在(0,+∞)递增,
∴f(x)>f(0)=0,
∴当x>0时,不等式1n(1+x)>x-$\frac{1}{2}$x2成立
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
4.已知数列{an}中,a1=1,(n+1)an+1=2(a1+a2+…+an)(n∈N+),则数列{an}的通项公式是( )
| A. | an=$\frac{n+1}{3}$ | B. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+2}{4},n≥2}\end{array}\right.$ | ||
| C. | an=$\frac{n+1}{2}$ | D. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$ |
5.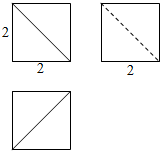 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{20}{3}$ | B. | 18 | C. | $24+2\sqrt{3}$ | D. | $18+2\sqrt{3}$ |
9.“x2-1>0”是“x>1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.据统计,夏季期间某旅游景点每天的游客人数服从正态分布N(1000,1002),则在此期间的某一天,该旅游景点的游客人数不超过1300的概率为( )
| A. | 0.4987 | B. | 0.8413 | C. | 0.9772 | D. | 0.9987 |
 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.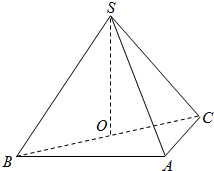 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.