题目内容
19.圆O1:x2+y2-6x-4y-3=0和圆O2:x2+y2-4y=0的位置关系是( )| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
分析 求出两个圆的圆心和半径,根据圆圆之间的位置关系的条件即可得到结论.
解答 解:圆O1:x2+y2-6x-4y-3=0,圆心为O1(3,2),半径为R=4,
圆O2:x2+y2-4y=0的标准方程为x2+(y-2)2=4,圆心为O2(0,2),半径为r=2,
则|O1O2|=$\sqrt{(3-0)^{2}+(2-2)^{2}}$=3,
∵R-r=2<3<R+r=6,
故圆O1和圆O2的位置关系是相交,
故选:B.
点评 本题主要考查圆与圆的位置关系的判断,求出圆的圆心和半径是解决本题的关键.

练习册系列答案
相关题目
9.若l,m,n是不相同的空间直线,α,β是不重合的两个平面,则下列命题正确的是( )
| A. | l⊥α,m⊥β,l⊥m⇒α⊥β | B. | l∥m,m⊆α⇒l∥α | ||
| C. | l⊆α,m⊆α,l∥β,m∥β⇒α∥β | D. | l⊥n,m⊥n⇒l∥m |
14.如果a>b>0,那么下列不等式成立的是( )
| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
4.已知数列{an}中,a1=1,(n+1)an+1=2(a1+a2+…+an)(n∈N+),则数列{an}的通项公式是( )
| A. | an=$\frac{n+1}{3}$ | B. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+2}{4},n≥2}\end{array}\right.$ | ||
| C. | an=$\frac{n+1}{2}$ | D. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$ |
11.一个正三棱锥的正视图及俯视图如图所示,则该三棱锥的左视图的面积为( )
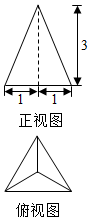

| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
8.已知某几何体的三视图如上图所示,则该几何体的体积为( )
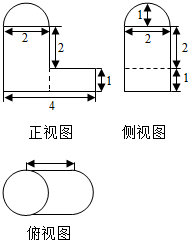

| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
9.“x2-1>0”是“x>1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |