题目内容
9.“?x∈R,x2-2>0”的否定是( )| A. | ?x∈R,x2-2<0 | B. | ?x∈R,x2-2≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$-2<0 | D. | ?x0∈R,x${\;}_{0}^{2}$-2≤0 |
分析 根据全称命题的否定是特称命题进行判断即可.
解答 解:命题是全称命题,则命题的否定是特称命题,
即?x0∈R,x${\;}_{0}^{2}$-2≤0,
故选:D.
点评 本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
4.已知数列{an}中,a1=1,(n+1)an+1=2(a1+a2+…+an)(n∈N+),则数列{an}的通项公式是( )
| A. | an=$\frac{n+1}{3}$ | B. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+2}{4},n≥2}\end{array}\right.$ | ||
| C. | an=$\frac{n+1}{2}$ | D. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$ |
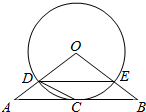 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.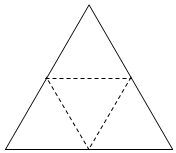 如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.
如图所示的平面图形是边长为8的正三角形,沿三边中点连线向同一方向折成一个多面体.

 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是$\frac{\sqrt{3}}{3}$,表面积是$\sqrt{3}$+1+$\sqrt{7}$.