题目内容
16.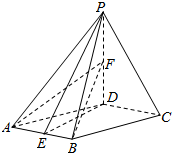 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.(1)证明平面PED⊥平面FAB;
(2)若PD=4,求三棱锥P-FAB的体积.
分析 (1)连接BD,可得AB⊥DE,由PD⊥平面ABCD,可得AB⊥PD,即可证明AB⊥平面PED,结合AB?平面FAB,从而可证平面PED⊥平面FAB.
(2)由PD=4,可求PF,FD,DE的值,进而可求VP-ABD,VF-ABD的值,利用VP-ABF=VP-ABD-VF-ABD即可计算得解.
解答 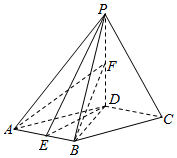 (本题满分为12分)
(本题满分为12分)
证明:(1)连接BD,
∵AB=AD,∠DAB=60°,
∴△ABC为等边三角形,
∵E是AB中点,
∴AB⊥DE,…2分
∵PD⊥平面ABCD,AB?平面ABCD,∴AB⊥PD,
∵DE?平面PED,PD?平面PED,DE∩PD=D,
∴AB⊥平面PED,…4分
∵AB?平面FAB,
∴平面PED⊥平面FAB.…6分
(2)∵PD=4,可求:PF=1,FD=3,DE=2$\sqrt{3}$,…10分
∴△DAB的面积为4$\sqrt{3}$,
∴VP-ABD=$\frac{16\sqrt{3}}{3}$,VF-ABD=4$\sqrt{3}$,…11分
∴VP-ABF=$\frac{16\sqrt{3}}{3}$-4$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.…12分
点评 本题主要考查了平面与平面垂直的判定,三棱锥体积的求法,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
4.已知数列{an}中,a1=1,(n+1)an+1=2(a1+a2+…+an)(n∈N+),则数列{an}的通项公式是( )
| A. | an=$\frac{n+1}{3}$ | B. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+2}{4},n≥2}\end{array}\right.$ | ||
| C. | an=$\frac{n+1}{2}$ | D. | an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{n+1}{3},n≥2}\end{array}\right.$ |
11.一个正三棱锥的正视图及俯视图如图所示,则该三棱锥的左视图的面积为( )
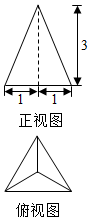

| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
8.已知某几何体的三视图如上图所示,则该几何体的体积为( )
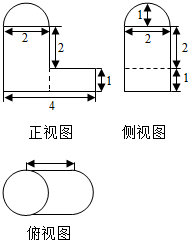

| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
5.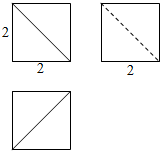 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
 棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )
棱长为2的正方体被一个平面截去一部分后所得的几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{20}{3}$ | B. | 18 | C. | $24+2\sqrt{3}$ | D. | $18+2\sqrt{3}$ |
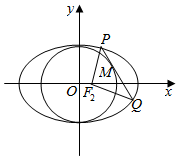 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上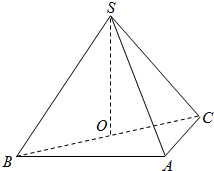 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.