题目内容
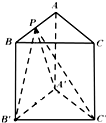 三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )
三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
考点:二面角的平面角及求法,两角和与差的正切函数
专题:空间角
分析:记P在A′B′=1上的投影为P′,A′P′=t,则B′P′=1-t,由图形得tanα=
=
,tanβ=
,由此能求出tan(α+β)的最小值.
| 1 | ||||
|
| 2 | ||
|
| 2 | ||
|
解答:
解:记P在A′B′=1上的投影为P′,A′P′=t,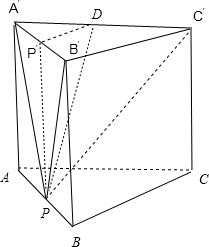
则B′P′=1-t,由图形得tanα=
=
,
tanβ=
,
∴tan(α+β)=
=
=
•
≥-
.
∴tan(α+β)的最小值是-
.
故选:C.

则B′P′=1-t,由图形得tanα=
| 1 | ||||
|
| 2 | ||
|
tanβ=
| 2 | ||
|
∴tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
=
| ||||||||
1-
|
=
| 2 | ||
|
| 1 | ||
t-t2-
|
≥-
8
| ||
| 13 |
∴tan(α+β)的最小值是-
8
| ||
| 13 |
故选:C.
点评:本题考查两角和的正切值的最小值的求法,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a>b,则下列不等式成立的是( )
A、
| ||||||
| B、a>|b| | ||||||
C、
| ||||||
| D、lna>lnb |
某学校从1208名学生中抽取20人参加义务劳动,规定采用下列方式选取:先用简单随机抽样的方法从1208人中剔除8人,剩下的1200人再按系统抽样的方法抽取,那么在1208人中每个人入选的概率为( )
A、都相等且等于
| ||
B、都相等且等于
| ||
| C、不全相等 | ||
| D、均不相等 |
甲乙两人进行乒乓球单打决赛,采用五局三胜制,对于每局比赛甲获胜的概率为
,乙获胜的概率为
,则爆出冷门(乙获冠军)的概率为( )
| 2 |
| 3 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在一次试验中,所抽取的样本共有5个个体,其值分别为0,1,2,3,a.若该样本的平均值为1,则样本的标准差为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|