题目内容
若a＞b，则下列不等式成立的是（ ）
A、
| ||||||
| B、a＞|b| | ||||||
C、
| ||||||
| D、lna＞lnb |
考点：基本不等式
专题：不等式的解法及应用
分析：举反例可排除B、C、D，可得答案．
解答：
解：举a=1，b=-2，显然满足a＞b，但a＜|b|，故B错误；
同样举a=1，b=-2，lnb无意义，故D错误；
还是a=1，b=-2，但有
＞
，故C错误，
而A，因为函数y=
为R上的增函数，显然有
＞
，
故选：A．
同样举a=1，b=-2，lnb无意义，故D错误；
还是a=1，b=-2，但有
| 1 |
| a |
| 1 |
| b |
而A，因为函数y=
| 3 | x |
| 3 | a |
| 3 | b |
故选：A．
点评：本题考查不等式的性质，举反例是解决问题的关键，属基础题．
练习册系列答案
相关题目
用“更相减损术”求98和63的最大公约数，要做减法的次数是（ ）
| A、3次 | B、4次 | C、5次 | D、6次 |
设函数f（x）=x3（x∈R），若0≤θ≤
时，f（m•sinθ）+f（1-m）＞0恒成立，则实数m的取值范围是（ ）
| π |
| 2 |
| A、（0，+∞） |
| B、（1，+∞） |
| C、（-∞，1） |
| D、[0，1] |
执行如图所示的框图，如果输入的x∈[0，
]，则输出的y值属于（ ）
| π |
| 2 |
| A、[0，1] | ||||
B、[0，
| ||||
C、[
| ||||
D、[
|
在△ABC中，角A，B，C所对应的边分别为a，b，c，若A=60°，b=1，且△ABC的面积为
，则边a的值为（ ）
| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、3 |
已知经过同一点的n（n∈N*，n≥3）个平面，任意三个平面不经过同一条直线．若这n个平面将空间分成f（n）个部分，则f（n）=（ ）
A、
| ||
B、
| ||
| C、n2-n+1 | ||
| D、n2-n+2 |
三角形两边长分别为1，
，第三边的中线长也是1，则三角形内切圆半径为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、3-
|
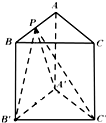三棱柱ABC-A′B′C′的底面是边长为1的正三角形，高AA′=1，在AB上取一点P，设△PA′C′与底面所成的二面角为α，△PB′C′与底面所成的二面角为β，则tan（α+β）的最小值是（ ）A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|