题目内容
甲乙两人进行乒乓球单打决赛，采用五局三胜制，对于每局比赛甲获胜的概率为
，乙获胜的概率为
，则爆出冷门（乙获冠军）的概率为（ ）
| 2 |
| 3 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：相互独立事件的概率乘法公式
专题：概率与统计
分析：分别求得乙胜了3局的概率、乙胜了4局的概率、乙胜了5局的概率，相加，即得所求．
解答：
解：乙获得冠军，包括三种情况：
①乙胜了3局，概率为
•(
)3(
)2=
；
②乙胜了4局，概率为
•(
)4
=
；
③乙胜了5局，概率为(
)5 =
，
故乙获得冠军的概率是
+
+
=
=
，
故选：A
①乙胜了3局，概率为
| C | 3 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| 40 |
| 243 |
②乙胜了4局，概率为
| C | 4 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| 10 |
| 243 |
③乙胜了5局，概率为(
| 1 |
| 3 |
| 1 |
| 243 |
故乙获得冠军的概率是
| 40 |
| 243 |
| 10 |
| 243 |
| 1 |
| 243 |
| 51 |
| 243 |
| 17 |
| 81 |
故选：A
点评：本题主要考查相互独立事件的概率乘法公式的应用，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
三角形两边长分别为1，
，第三边的中线长也是1，则三角形内切圆半径为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、3-
|
a=log9
，b=log8
，c=
，则a，b，c的大小关系是（ ）
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、a＞c＞b |
| D、b＞c＞a |
在△ABC中角A、B、C的对边分别是a、b、c，已知2acosB=c，那么△ABC一定是（ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、正三角形 |
设a＞0，b＞0，
是2a与2b的等比中项，则
+
的最小值为（ ）
| 2 |
| 1 |
| a |
| 4 |
| b |
| A、10 | B、9 | C、8 | D、7 |
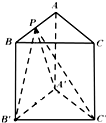三棱柱ABC-A′B′C′的底面是边长为1的正三角形，高AA′=1，在AB上取一点P，设△PA′C′与底面所成的二面角为α，△PB′C′与底面所成的二面角为β，则tan（α+β）的最小值是（ ）A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|