题目内容
在一次试验中,所抽取的样本共有5个个体,其值分别为0,1,2,3,a.若该样本的平均值为1,则样本的标准差为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:极差、方差与标准差
专题:概率与统计
分析:根据已知中数据,代入平均数公式,计算出a值,进而代入标准差计算公式,可得答案.
解答:
解:∵样本a,0,1,2,3的平均值为1,
∴
(0+1+2+3+a)=
=1,
解得a=-1,
则样本的标准差s=
=
,
故选:D.
∴
| 1 |
| 5 |
| a+6 |
| 5 |
解得a=-1,
则样本的标准差s=
|
| 2 |
故选:D.
点评:本题考查的知识点是标准差与平均数,熟练掌握标准差的计算公式是解答的关键.

练习册系列答案
相关题目
执行如图所示的框图,如果输入的x∈[0,
],则输出的y值属于( )

| π |
| 2 |

| A、[0,1] | ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
若
<
<0,则下列不等式:①|a|>|b|;②a+b>ab;③
+
>2;④
<2a-b中,正确的不等式是( )
| 1 |
| a |
| 1 |
| b |
| a |
| b |
| b |
| a |
| a2 |
| b |
| A、①② | B、③④ | C、①③ | D、②④ |
在△ABC中角A、B、C的对边分别是a、b、c,已知2acosB=c,那么△ABC一定是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、正三角形 |
函数f(x)=
,则f′(-4)=( )
| 1-2x |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
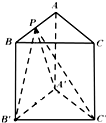 三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )
三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
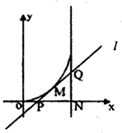 函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P、Q,点N(1,0),设△PQN的面积为S=g(t).
函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P、Q,点N(1,0),设△PQN的面积为S=g(t).