题目内容
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=
x3-
x+8(0<x≤120),已知甲、乙两地相距100千米.
(Ⅰ)求汽车从甲地到乙地匀速行驶的耗油量S(升)与行驶速度x(千米/小时)的函数关系式;
(Ⅱ)当汽车以多大速度匀速行驶时,从甲地到乙地的耗油量S最少?最少为多少升?
| 1 |
| 128000 |
| 3 |
| 80 |
(Ⅰ)求汽车从甲地到乙地匀速行驶的耗油量S(升)与行驶速度x(千米/小时)的函数关系式;
(Ⅱ)当汽车以多大速度匀速行驶时,从甲地到乙地的耗油量S最少?最少为多少升?
考点:根据实际问题选择函数类型
专题:应用题,导数的综合应用
分析:(Ⅰ)当速度为x千米/小时时,汽车从甲地到乙地行驶了
小时,即可求出耗油量为h(x)与速度为x的关系式;
(Ⅱ)利用导函数求出S的极小值判断出就是最小值即可.
| 100 |
| x |
(Ⅱ)利用导函数求出S的极小值判断出就是最小值即可.
解答:
解:(Ⅰ)当速度为x千米/小时时,汽车从甲地到乙地行驶了
小时,则
依题意得S=(
x3-
x+8)•
=
x2+
-
(0<x≤120);
(Ⅱ)S′=
(0<x≤120).
令S′=0,得x=80.
当x∈(0,80)时,S′<0,S是减函数;
当x∈(80,120)时,S′>0,S是增函数.
∴当x=80时,S取到极小值11.25.
∵S在(0,120]上只有一个极值,
∴它是最小值.
故当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
| 100 |
| x |
依题意得S=(
| 1 |
| 128000 |
| 3 |
| 80 |
| 100 |
| x |
| 1 |
| 1280 |
| 800 |
| x |
| 15 |
| 4 |
(Ⅱ)S′=
| x3-803 |
| 640x2 |
令S′=0,得x=80.
当x∈(0,80)时,S′<0,S是减函数;
当x∈(80,120)时,S′>0,S是增函数.
∴当x=80时,S取到极小值11.25.
∵S在(0,120]上只有一个极值,
∴它是最小值.
故当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
点评:本小题主要考查函数、导数及其应用等基本知识,考查运用数学知识分析和解决实际问题的能力.

练习册系列答案
相关题目
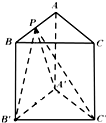 三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )
三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
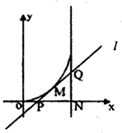 函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P、Q,点N(1,0),设△PQN的面积为S=g(t).
函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P、Q,点N(1,0),设△PQN的面积为S=g(t).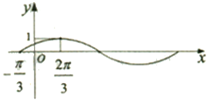 已知函数f(x)=sin(ωx+φ)(其中ω>0,φ∈(-
已知函数f(x)=sin(ωx+φ)(其中ω>0,φ∈(-