题目内容
(1)在曲线y=
上找一点P,使P点到直线x-4y+14=0的距离最短,求出最短距离及此时P点的坐标.
(2)求过点(-1,-1)且和曲线y=1+2x-x3相切的直线方程.
| x |
(2)求过点(-1,-1)且和曲线y=1+2x-x3相切的直线方程.
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:(1)由曲线y=
上点P的切线平行于x-4y+14=0,可得P点的坐标,从而求出最短距离;
(2)设切点(x0,y0),根据直线过点(-1,-1)且和曲线y=1+2x-x3相切,建立方程,求出切点,即可求过点(-1,-1)且和曲线y=1+2x-x3相切的直线方程.
| x |
(2)设切点(x0,y0),根据直线过点(-1,-1)且和曲线y=1+2x-x3相切,建立方程,求出切点,即可求过点(-1,-1)且和曲线y=1+2x-x3相切的直线方程.
解答:
解:(1)设P(m,n),则
∵y=
,∴y′=
,
由
=
,可得m=4,∴n=2,
此时P(4,2)到直线x-4y+14=0的距离最短,最短距离为d=
=
;
(2)设切点(x0,y0),则2-3x02=
,
∴2x02(x0+
)=0,
∴x0=0,或x0=-
,
x0=0,切线为y=2x+1;
x0=-
,切线为19x+4y+23=0.
∵y=
| x |
| 1 | ||
2
|
由
| 1 | ||
2
|
| 1 |
| 4 |
此时P(4,2)到直线x-4y+14=0的距离最短,最短距离为d=
| |4-8+14| | ||
|
10
| ||
| 17 |
(2)设切点(x0,y0),则2-3x02=
| 1+2x0-x03+1 |
| x0+1 |
∴2x02(x0+
| 3 |
| 2 |
∴x0=0,或x0=-
| 3 |
| 2 |
x0=0,切线为y=2x+1;
x0=-
| 3 |
| 2 |
点评:本题考查利用导数研究曲线上某点切线方程,考查利用导数研究曲线上某点切线方程,考查学生的计算能力,难度中等.

练习册系列答案
相关题目
在△ABC中,角A,B,C所对应的边分别为a,b,c,若A=60°,b=1,且△ABC的面积为
,则边a的值为( )
| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、3 |
a=log9
,b=log8
,c=
,则a,b,c的大小关系是( )
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| A、a>b>c |
| B、b>a>c |
| C、a>c>b |
| D、b>c>a |
设a>0,b>0,
是2a与2b的等比中项,则
+
的最小值为( )
| 2 |
| 1 |
| a |
| 4 |
| b |
| A、10 | B、9 | C、8 | D、7 |
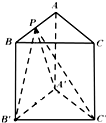 三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )
三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面所成的二面角为α,△PB′C′与底面所成的二面角为β,则tan(α+β)的最小值是( )A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
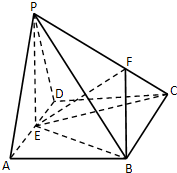 如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=
如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=