题目内容
某种汽车购买时费用为16.9万元，每年应交付保险费、汽油费费用共1.5万元，汽车的维修费用为：第一年0.4万元，第二年0.6万元，第三年0.8万元，…依等差数列逐年递增．
（1）设该车使用n年的总费用（包括购车费用）为f（n），试写出f（n）的表达式；
（2）求这种汽车使用多少年报废最合算（即该车使用多少年平均费用最少）．
（1）设该车使用n年的总费用（包括购车费用）为f（n），试写出f（n）的表达式；
（2）求这种汽车使用多少年报废最合算（即该车使用多少年平均费用最少）．
考点：基本不等式在最值问题中的应用,数列的应用
专题：应用题,不等式的解法及应用
分析：（I）由已知，根据等差数列前n项和公式，即可得到f（n）的表达式；
（II）由（I）中使用n年该车的总费用，我们可以得到n年平均费用表达式，根据基本不等式，我们易计算出平均费用最小时的n值，进而得到结论．
（II）由（I）中使用n年该车的总费用，我们可以得到n年平均费用表达式，根据基本不等式，我们易计算出平均费用最小时的n值，进而得到结论．
解答：
解：（1）依题意f（n）=16.9+（0.2+0.4+0.6+…+0.2n）+1.5n=0.1n2+1.8n+16.9（n∈N*）；
（Ⅱ）设该车的年平均费用为S万元，则有S=
=0.1n+
+1.8
≥2
+1.8=4.4
当且仅当0.1n+
，即n=13时，等号成立．
所以，这种汽车使用13年报废最合算．
（Ⅱ）设该车的年平均费用为S万元，则有S=
| f(n) |
| n |
| 16.9 |
| n |
≥2
| 1.69 |
当且仅当0.1n+
| 16.9 |
| n |
所以，这种汽车使用13年报废最合算．
点评：本题考查的知识点是根据实际问题选择函数类型，基本不等式在最值问题中的应用，数列的应用，其中（I）的关键是由等差数列前n项和公式，得到f（n）的表达式，（II）的关键是根据基本不等式，得到函数的最小值点．
练习册系列答案
相关题目
三角形两边长分别为1，
，第三边的中线长也是1，则三角形内切圆半径为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、3-
|
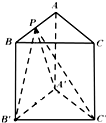三棱柱ABC-A′B′C′的底面是边长为1的正三角形，高AA′=1，在AB上取一点P，设△PA′C′与底面所成的二面角为α，△PB′C′与底面所成的二面角为β，则tan（α+β）的最小值是（ ）A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
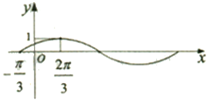已知函数f（x）=sin（ωx+φ）（其中ω＞0，φ∈（-