题目内容
函数f(x)=
,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有下列结论:
①m∈[3,4);
②abcd∈[0,e4);
③a+b+c+d∈[e5+
-2,e6+
-2);
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
其中正确的结论个数为( )
|
①m∈[3,4);
②abcd∈[0,e4);
③a+b+c+d∈[e5+
| 1 |
| e |
| 1 |
| e2 |
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
其中正确的结论个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:分段函数的应用,函数的图象
专题:函数的性质及应用
分析:对于①画出y=f(x)与y=m的图象即可;对于②,结合图象把abcd的不等式用m表示出来
对于③同样用m把a+b+c+d表示出来;对于④若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,画图即可.
对于③同样用m把a+b+c+d表示出来;对于④若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,画图即可.
解答:
解:∵f(x)=
=
∴函数f(x)的图象如下

若直线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈[3,4),故①正确
四个交点横坐标从小到大,依次记为a,b,c,d,则a,b是x2+2x+m-3=0
的两根,∴a+b=-2,ab=m-3,∴ab∈[0,1),且lnc=2-m,lnd=2+m,∴ln(cd)=4∴cd=e4,
∴abcd∈[0,e4),∴②是正确的.由2-lnx=4得x=
,由2-lnx=3得x=
,∴c∈(
,
],又∵cd=e4,
∴a+b+c+d=c+
-2在(
,
]是递减函数,∴a+b+c+d∈[e5+
-2,e6+
-2);
∴③是正确的
若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,
而直线y=-x+3 与y=-x+
均与y=f(x)有三个交点,∴m不唯一.∴④是不正确的
故选C
|
|

若直线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈[3,4),故①正确
四个交点横坐标从小到大,依次记为a,b,c,d,则a,b是x2+2x+m-3=0
的两根,∴a+b=-2,ab=m-3,∴ab∈[0,1),且lnc=2-m,lnd=2+m,∴ln(cd)=4∴cd=e4,
∴abcd∈[0,e4),∴②是正确的.由2-lnx=4得x=
| 1 |
| e2 |
| 1 |
| e |
| 1 |
| e2 |
| 1 |
| e |
∴a+b+c+d=c+
| e4 |
| c |
| 1 |
| e2 |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e2 |
∴③是正确的
若关于x的方程f(x)+x=m恰有三个不同实根,则y=f(x)与y=-x+m有三个不同的交点,
而直线y=-x+3 与y=-x+
| 15 |
| 4 |
故选C
点评:本题考查函数的图象,分段函数,零点与方程的根之间的关系,综合性较强.

练习册系列答案
相关题目
若抛物线y=ax2的焦点为F(0,1),则a的值为( )
A、
| ||
| B、4 | ||
C、
| ||
| D、2 |
已知双曲线的一个焦点坐标为(
,0),且经过点(-5,2),则双曲线的标准方程为( )
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若数列{an}的前n项和Sn满足Sn=4-an(n∈N*),则a5=( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
数列1,3,6,10,x,21,…中,x的值是 ( )
| A、12 | B、13 | C、15 | D、16 |
 已知函数f(x)=Asin(
已知函数f(x)=Asin(| π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知点D是△ABC的边BC上的中点,且|
|=4,|
|=2,则
•
=( )
| AC |
| AB |
| AD |
| BC |
| A、2 | ||
| B、4 | ||
| C、6 | ||
D、2
|
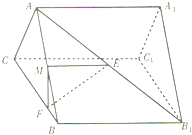 如图,直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1的各棱长都相等,M、E分别是AB和AB1的中点,点F在BC上,且满足BF=1,FC=3.
如图,直三棱柱(侧棱垂直于底面的三棱柱)ABC-A1B1C1的各棱长都相等,M、E分别是AB和AB1的中点,点F在BC上,且满足BF=1,FC=3.