题目内容

过双曲线x2-y2=1的右焦点且与右支有两个交点的直线，其倾斜角范围是
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：把直线方程与双曲线方程联立消去y，根据x1x2＞0，x1+x2＞0和判别式大于0求得k的范围．
解答： 解：设直线y=kx+
2
，与双曲线方程联立，消去y，可得（1-k2）x2-2
2
kx-3=0
∵x1x2＞0  
∴-
3
1-k2
＞0，
∴k2＞1，即k＞1或者k＜-1①
又x1+x2＞0，∴
2
2
k
1-k2
＞0，可得k＜0，②
又△=（8k2）+12（1-k2）＞0解得-
3
＜k＜
3
③
由①②③知k的取值范围是-
3
＜k＜-1．
故答案为：-
3
＜k＜-1．
点评：本题主要考查了直线与圆锥曲线的综合问题．当直线与圆锥曲线相交，涉及交点问题时常用“韦达定理法”来解决．
练习册系列答案
相关题目
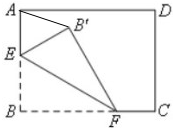如图，在矩形ABCD中，AB=3，BC=4，点E、F分别在AB、BC边上，将△BEF沿EF折叠，点B落在B′处，当B′在矩形ABCD内部时，AB′的最小值为
 
．
曲线y2=x与y=x2所围成的图形的面积是
 
．
北京市各级各类中小学每年都要进行“学生体质健康测试”，测试总成绩满分为100分，规定测试成绩在[85，100]之间为体质优秀；在[75，85）之间为体质良好；在[60，75）之间为体质合格；在[0，60）之间为体质不合格．现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩，其茎叶图如下：
 9  1  3  5  6                        
 8  0  1  1  2  2  3  3  3  4  4 5   6  6  7  7  9
 7  0  5  6  6  7  9                    
 6  4  5  8                          
 5  6                              
（Ⅰ）试估计该校高三年级体质为优秀的学生人数；
（Ⅱ）根据以上30名学生体质健康测试成绩，现采用分层抽样的方法，从体质为优秀和良好的学生中抽取5名学生，再从这5名学生中选出3人．
（ⅰ）求在选出的3名学生中至少有1名体质为优秀的概率；
（ⅱ）求选出的3名学生中体质为优秀的人数不少于体质为良好的人数的概率．
已知函数f（x）=a2x-4+n（a＞0且a≠1）且的图象恒过定点P（m，2），则m+n=
 
．
已知等差数列{an}中，a5=5，a1=1，则数列{
1
anan+1
}的前50项和为
 
．
已知函数f(x)=
ex(x≤0)
lnx     (x＞0)
，则函数y=f[f（x）]-1的零点个数为（　　）
A、1B、2C、3D、4
已知向量
a
=（
3
，1），
b
=（1，c）．若
a
•
b
=0，则实数c的值为（　　）
A、-
3
B、
3
C、
3
3
D、-
3
3
函数f（x）=
-x2-2x+3，x≤0
|2-lnx|，x＞0
，直线y=m与函数f（x）的图象相交于四个不同的点，从小到大，交点横坐标依次记为a，b，c，d，有下列结论：
①m∈[3，4）；
②abcd∈[0，e4）；
③a+b+c+d∈[e5+
1
e
-2，e6+
1
e2
-2）； 
④若关于x的方程f（x）+x=m恰有三个不同实根，则m取值唯一．
其中正确的结论个数为（　　）
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网