题目内容
函数y=|（
）x-1|的单调递增区间是 ．
| 1 |
| 2 |
考点：复合函数的单调性
专题：作图题,函数的性质及应用
分析：作出函数y=|（
）x-1|的图象，由图可得函数y=|（
）x-1|的单调递增区间．
| 1 |
| 2 |
| 1 |
| 2 |
解答：
解：作出函数y=|（
）x-1|的图象，
由图可知，函数y=|（
）x-1|的单调递增区间是[0，+∞），
故答案为：[0，+∞）．
| 1 |
| 2 |
由图可知，函数y=|（
| 1 |
| 2 |
故答案为：[0，+∞）．
点评：本题考查复合函数的单调性，着重考查指数函数与绝对值函数的复合，作图是关键，考查作图与分析能力，属于中档题．
练习册系列答案
相关题目
全集U={1，2，3，4，5，6}，A={1，3}，B={2，4}，C={1，2，5，6}，则（A∪B）∩∁UC=（ ）
| A、{1，2} |
| B、{3，4} |
| C、{1，2，3，4} |
| D、{3，4，5，6} |
已知函数y=f（x）的定义域是数集A，若对于任意a，b∈A，当a＜b时，都有f（a）＜f（b），则方程f（x）的实数根为（ ）
| A、有且只有一个 |
| B、一个都没有 |
| C、至多有一个 |
| D、可能会有两个或两个以上 |
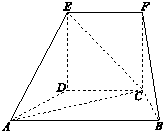如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，AB=2BC，∠ABC=60°，且平面CDEF⊥平面ABCD．