题目内容
△ABC中，
=
，边AC的中点为E，△ABC的中线AM与DE相交于N，设
=
，
=
，请用
，
表示
= ．
| AD |
| 2 |
| 3 |
| AB |
| AB |
| a |
| AC |
| b |
| a |
| b |
| BN |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：A，N，M三点共线，所以得到向量
∥
，所以存在实数λ使
=λ
，根据向量的减法及共线向量基本定理并带入
，
便可得到：
=(
-1)
+
；
同样根据三点D，N，E共线可得，存在实数μ使
=-
+
，根据平面向量基本定理可得
，这样解出λ，μ即可用
，
表示出
．
| AN |
| AM |
| AN |
| AM |
| a |
| b |
| BN |
| λ |
| 2 |
| a |
| λ |
| 2 |
| b |
同样根据三点D，N，E共线可得，存在实数μ使
| BN |
| 1+2μ |
| 3 |
| a |
| μ |
| 2 |
| b |
|
| a |
| b |
| BN |
解答：
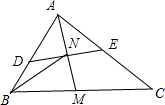解：如图，A，N，M三点共线，∴
，
共线，∴存在实数λ使：
=λ
，∴(
-
)=λ(
-
)；
∴
=(1-λ)
+λ
=(λ-1)
+
=(λ-1)
+
(
-
)=(
-1)
+
；
同理，D，N，E三点共线，存在μ使
=(1-μ)
+μ
=
+μ(
+
)=-
+
=-
+
；
∴
，解得λ=μ=
；
∴
=-
+
．
解：如图，A，N，M三点共线，∴| AN |
| AM |
| AN |
| AM |
| BN |
| BA |
| BM |
| BA |
∴
| BN |
| BA |
| BM |
| AB |
| λ |
| 2 |
| BC |
| AB |
| λ |
| 2 |
| AC |
| AB |
| λ |
| 2 |
| a |
| λ |
| 2 |
| b |
同理，D，N，E三点共线，存在μ使
| BN |
| BD |
| BE |
| 1-μ |
| 3 |
| BA |
| BA |
| AE |
| 1+2μ |
| 3 |
| AB |
| μ |
| 2 |
| AC |
| 1+2μ |
| 3 |
| a |
| μ |
| 2 |
| b |
∴
|
| 4 |
| 7 |
∴
| BN |
| 5 |
| 7 |
| a |
| 2 |
| 7 |
| b |
点评：考查共线向量基本定理，向量的减法运算，共面向量基本定理．
练习册系列答案
相关题目
下列函数既是奇函数，又在区间[-1，1]上单调递减的是（ ）
| A、f（x）=sinx | ||
| B、f（x）=-|x+1| | ||
C、f（x）=
| ||
D、f（x）=ln
|