题目内容
已知二次函数y=f(x)的图象经过坐标原点,其导函数f ′(x)=2x+2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn=2n·an,Tn是数列{bn}的前n项和,求Tn.
(1)设f(x)=ax2+bx,f ′(x)=2ax+b=2x+2,
∴a=1,b=2,f(x)=x2+2x,
∴Sn=n2+2n,
∴当n≥2时,an=Sn-Sn-1=(n2+2n)-[(n-1)2+2(n-1)]=2n+1,
又a1=S1=3,适合上式,∴an=2n+1.
(2)bn=(2n+1)·2n,
∴Tn=3·21+5·22+7·23+…+(2n+1)·2n,
∴2Tn=3·22+5·23+7·24+…+(2n+1)·2n+1,
相减得-Tn=3·21+2·(22+23+…+2n)-(2n+1)·2n+1
=6+2·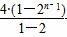 -(2n+1)·2n+1
-(2n+1)·2n+1
=(1-2n)·2n+1-2,
∴Tn=(2n-1)·2n+1+2.

练习册系列答案
相关题目
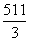 ,若从中去掉一项am,剩下的8项的平均值等于
,若从中去掉一项am,剩下的8项的平均值等于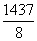 ,则m等于( )
,则m等于( )

 B.
B. C.
C. D.
D.