题目内容
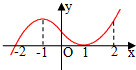 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①-2是函数y=f(x)的极值点
②1是函数y=f(x)的极小值点
③y=f(x)在x=0处切线的斜率大于零
④y=f(x)在区间(-∞,-2)上单调递减
则正确命题的序号是
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:根据函数单调性与导数之间的关系进行判断即可得到结论.
解答:
解:①由导数图象可知,当x<-2时,f′(x)<0,函数单调递减,当x>-2时,f′(x)>0,函数单调递增,
∴-2是函数y=f(x)的极小值点,∴①正确.
②当x>-2时,f′(x)>0,函数单调递增,
∴1是函数y=f(x)的极小值点,错误.
③当x>-2时,f′(x)>0,函数单调递增,
∴y=f(x)在x=0处切线的斜率大于零,∴③正确.
④当x<-2时,f′(x)<0,函数单调递减,
∴y=f(x)在区间(-∞,-2)上单调递减,∴④正确.
则正确命题的序号是 ①③④,
故答案为:①③④
∴-2是函数y=f(x)的极小值点,∴①正确.
②当x>-2时,f′(x)>0,函数单调递增,
∴1是函数y=f(x)的极小值点,错误.
③当x>-2时,f′(x)>0,函数单调递增,
∴y=f(x)在x=0处切线的斜率大于零,∴③正确.
④当x<-2时,f′(x)<0,函数单调递减,
∴y=f(x)在区间(-∞,-2)上单调递减,∴④正确.
则正确命题的序号是 ①③④,
故答案为:①③④
点评:本题主要考查导数的应用,利用导数图象,判断函数的单调性是解决本题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
(3-2i)÷(2+3i)=( )
| A、i | B、-1 | C、-i | D、1 |
下列命题中的真命题是( )
| A、对于实数a、b、c,若a>b,则ac2>bc2 | ||
| B、x2>1是x>1的充分而不必要条件 | ||
| C、?α,β∈R,使得sin(α+β)=sinα+sinβ成立 | ||
D、?α,β∈R,tan(α+β)=
|
某产品共有三个等级,分别为一等品、二等品和不合格品.从一箱产品中随机抽取1件进行检测,设“抽到一等品”的概率为0.65,“抽到二等品”的概率为0.3,则“抽到不合格品”的概率为( )
| A、0.95 | B、0.7 |
| C、0.35 | D、0.05 |
(1+x)(1-x)(2-x)5的展开式含x2项的系数是( )
| A、-80 | B、48 | C、80 | D、78 |
