题目内容

已知函数f（x）=
(a2-1)log2(x+2)，-2＜x≤0
ax2+1，x＞0
在（-2，+∞）上是单调函数，则a的取值范围是
 
．
考点：函数单调性的性质
专题：计算题,函数的性质及应用
分析：根据函数f（x）=
(a2-1)log2(x+2)，-2＜x≤0
ax2+1，x＞0
在（-2，+∞）上是单调函数，可得
a2-1＞0
a＞0
1≥a2-1
或
a2-1＜0
a＜0
1≤a2-1
，求出a，即可求出a的取值范围．
解答： 解：由题意，
a2-1＞0
a＞0
1≥a2-1
或
a2-1＜0
a＜0
1≤a2-1
，
∴1＜a≤
2
，
故答案为：1＜a≤
2
．
点评：本题考查函数单调性的性质，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
若不等式x2-px+q=0的解集为（-
1
2
，
1
3
），则不等式qx2+px+1＞0的解集为（　　）
A、（-3，2）
B、（-2，3）
C、（-
1
3
，
1
2
）
D、（-
1
2
，
1
3
）
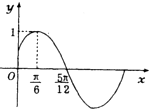已知函数f（x）=Asin（ωx+φ）（a＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则f（x）的解析式是（　　）
A、f（x）=sin（3x+
π
3
）
B、f（x）=sin（2x+
π
3
）
C、f（x）=sin（x+
π
3
）
D、f（x）=sin（2x+
π
6
）
已知直线l经过直线3x+4y-2=0与直线2x+y+2=0的交点P，且与直线x-2y-m=0的距离为
5
，求实数m的值．
已知n∈N*，且（-
1
4
）n＜（-
1
3
）n，则n的最小值是
 
．
求函数y=
1
2
log 
1
2
2x+log 
1
2
x+5在区间[2，8]上的最大值和最小值．
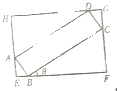如图，矩形ABCD的长AB=a，宽AD=b，外接矩形EFGH的面积为S，设∠CBF=θ．
（1）用θ表示S；
（2）求S的最大值．
若复数
2-bi
1+2i
的实部和虚部都互为相反数，则实数b=
 
．
已知p：-2≤
4-x
3
≤2，q：x2-2x+1-m2≤0（m＞0），若￢p是￢q的必要不充分条件，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网