题目内容
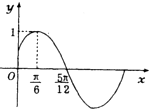已知函数f（x）=Asin（ωx+φ）（a＞0，ω＞0，|φ|＜| π |
| 2 |
A、f（x）=sin（3x+
| ||
B、f（x）=sin（2x+
| ||
C、f（x）=sin（x+
| ||
D、f（x）=sin（2x+
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：根据图象确定A，ω 和φ的值即可求函数的解析式．
解答：
解：由图象知函数的最大值为1，即A=1，
函数的周期T=4（
-
）=4×
=π=
，
解得ω=2，即f（x）=2sin（2x+φ），
由五点对应法知2×
+φ=
，
解得φ=
，
故f（x）=sin（2x+
），
故选：D
函数的周期T=4（
| 5π |
| 12 |
| π |
| 6 |
| 3π |
| 12 |
| 2π |
| ω |
解得ω=2，即f（x）=2sin（2x+φ），
由五点对应法知2×
| π |
| 6 |
| π |
| 2 |
解得φ=
| π |
| 6 |
故f（x）=sin（2x+
| π |
| 6 |
故选：D
点评：本题主要考查函数解析式的求解，根据条件确定A，ω 和φ的值是解决本题的关键．要要求熟练掌握五点对应法．
练习册系列答案
相关题目
若框图所给的程序运行结果为S=20，那么判断框中应填入的关于k的条件是（ ）
| A、k＞8？ | B、k≤8？ |
| C、k＜8？ | D、k=9？ |