题目内容
设函数f（x）=
+ax，当a≥1时，求函数f（x）在[0，+∞）的单调性．
| x2+1 |
考点：利用导数研究函数的单调性,函数单调性的判断与证明
专题：导数的综合应用
分析：求f′（x），判断f′（x）的符号，从而判断f（x）在[0，+∞）上的单调性．
解答：
解：f′（x）=
+a；
∴a≥1，x≥0时，f′（x）＞0；
∴f（x）在[0，+∞）上单调递增．
| x | ||
|
∴a≥1，x≥0时，f′（x）＞0；
∴f（x）在[0，+∞）上单调递增．
点评：考查通过判断导数符号判断函数单调性的方法，对f（x）的正确求导是求解本题的关键．
练习册系列答案
相关题目
关于全称命题与特称命题下列说法中不正确的一个为（ ）
| A、全称命题，对于取值集合中的每一个元素，命题都成立或都不成立 |
| B、特称命题，对于取值集合中至少有一个元素使命题成立或不成立 |
| C、“全称命题”的否定一定是“特称命题” |
| D、“特称命题”的否定一定不是“全称命题” |
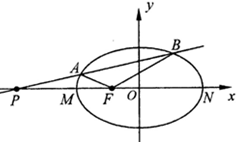如图，点F是椭圆