题目内容
9.已知函数$f(x)=ln\frac{1+x}{1-x}+{x^3}$,若函数y=f(x)+f(k-x2)有两个零点,则实数k的取值范围是( )| A. | $({-\frac{1}{4},+∞})$ | B. | $({-\frac{1}{4},0})$ | C. | $({-\frac{1}{4},2})$ | D. | $[{-\frac{1}{4},2}]$ |
分析 判断函数$f(x)=ln\frac{1+x}{1-x}+{x^3}$在区间(-1,1)上单增,且是奇函数;利用y=f(x)+f(k-x2)有两个零点,等价于方程x2-x-k=0在区间(-1,1)上有两个零点,列出不等式组求解即可.
解答 解:根据题意,可知$f(x)=ln\frac{1+x}{1-x}+{x^3}$在区间(-1,1)上单增,且是奇函数;
由函数y=f(x)+f(k-x2)有两个零点,
等价于方程x2-x-k=0在区间(-1,1)上有两个零点,
令g(x)=x2-x-k,则满足$\left\{\begin{array}{l}△>0\\ g(-1)>0\\ g(1)>0\end{array}\right.$,得$-\frac{1}{4}<k<0$.
故选:B.
点评 本题考查函数的单调性以及函数的奇偶性,函数的零点判定定理的应用,考查计算能力.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
20.在区间[-3,3]上随机选取一个实数x,则事件“2x-3<0”发生的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
14.不等式|x|+|3y|-6≤0所对应的平面区域的面积为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
1.已知双曲线Γ:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一条渐近线为l,圆C:(x-a)2+y2=8与l交于A,B两点,若△ABC是等腰直角三角形,且$\overrightarrow{OB}=5\overrightarrow{OA}$(其中O为坐标原点),则双曲线Γ的离心率为( )
| A. | $\frac{{2\sqrt{13}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{5}$ | C. | $\frac{{\sqrt{13}}}{5}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
18.某几何体的三视图如图,则该几何体的体积为( )
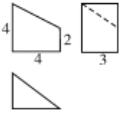

| A. | 18 | B. | 20 | C. | 24 | D. | 12 |