题目内容
19.已知函数f(x)=2ex-2-2ax-x2(x≥0)(1)当a=1时,求f(x)的单调区间,并证明此时f(x)≥0成立;
(2)若f(x)≥0在x∈[0,+∞)上恒成立,求a 的取值范围.
分析 (1)当a=1时,设g(x)=f′(x)=2(ex-x-1),g′(x)=2(ex-1)≥0,(x≥0),由此利用导数性质能求出f(x)的单调区间,并证明此时f(x)≥0成立.
(2)法一:当a≤1时,f′(x)=2(ex-x-a)≥0,从而f(x)≥0恒成立,x∈[0,+∞);当a>1时,设h(x)=f′(x)=2(ex-a-x),h′(x)=2(ex-1)≥0,(x≥0),由此利用导数性质能求出a的取值范围.
法二:(分离变量法)x=0时f(0)=0,x>0时f(x)≥0?a≤$\frac{{{e^x}-1-\frac{1}{2}{x^2}}}{x}$=g(x),g′(x)=$\frac{{x{e^x}-{e^x}+1-\frac{1}{2}{x^2}}}{x^2}$,令h(x)=xex-ex+1-$\frac{1}{2}$x2,h′(x)=x(ex-1)>0,由此利用洛比达法则能求出a的取值范围.
解答 解:(1)当a=1时,设g(x)=f′(x)=2(ex-x-1),g′(x)=2(ex-1)≥0,(x≥0)
∴f′(x)在[0,+∞)上递增,即x≥0时f′(x)≥f′(0)=0,
∴f(x)的增区间为[0,+∞),无减区间,
且x≥0时,f(x)=2ex-2-2x-x2≥f(0)=0.
(2)解法一:①当a≤1时,f′(x)=2(ex-x-a)≥2(x+1-x-a)=2(1-a)≥0,
∴x≥0时f(x)≥f(0)=0,
即当a≤1时,f(x)≥0恒成立,x∈[0,+∞),
②当a>1时,设h(x)=f′(x)=2(ex-a-x),h′(x)=2(ex-1)≥0,(x≥0),
∴f′(x)在[0,+∞)上递增,
又f′(0)=2(1-a)<0,f′(a)=2(ea-2a),
由(1)已证2ex-2-2x-x2≥0,知ex≥1+x+$\frac{1}{2}$x2,
∴f′(a)≥2(1+a+$\frac{1}{2}$a2-2a)=(a-1)2+1>0,
∴f′(x)在(0,a)上存在唯一零点xo,即${e^{x_o}}$-a-x0=0,
∴f(x)在(0,xo)上递减,在(xo,+∞)上递增,
又f(xo)=2${e^{x_o}}$-2-2axo-xo2=2(${e^{x_o}}$-1-x0${e^{x_o}}$+$\frac{1}{2}$xo2),
令g(x)=ex-1-xex+$\frac{1}{2}$x2,x∈(0,a),g′(x)=x(1-ex)<0,
∴当x>0时g(x)<g(0)=0,即f(xo)<0,
不满足f(x)≥0恒成立,由①②可知a的取值范围为(-∞,1].
解法二:(分离变量法)
x=0时f(0)=0,x>0时f(x)≥0?a≤$\frac{{{e^x}-1-\frac{1}{2}{x^2}}}{x}$=g(x),
g′(x)=$\frac{{x{e^x}-{e^x}+1-\frac{1}{2}{x^2}}}{x^2}$,
令h(x)=xex-ex+1-$\frac{1}{2}$x2,h′(x)=x(ex-1)>0,
∴x>0时h(x)>h(0)=0,
∴g′(x)>0,即g(x)在(0,+∞)上递增,
由洛比达法则$\begin{array}{l}{lim}\\{x→{0^+}}\end{array}$g(x)=$\begin{array}{l}{lim}\\{x→{0^+}}\end{array}$(ex-x)=1(适用于参加自主招生学生),
∴a的取值范围为(-∞,1].
点评 本题考查函数的单调区间的求法,实数取值范围的求法,考查不等式的证明,考查导数性质,考查推理论证能力、运算求解能力,考查转化化归思想、分类讨论思想,考查函数与方程思想,是中档题.

| A. | {1,2,3} | B. | {1,2} | C. | [1,2] | D. | [1,3) |
| A. | $\frac{16}{5}$ | B. | $\frac{16}{15}$ | C. | $\frac{16}{29}$ | D. | $\frac{16}{31}$ |
| A. | $\frac{17}{6}π$ | B. | $\frac{19}{6}π$ | C. | $\frac{17}{3}π$ | D. | $\frac{19}{3}π$ |
| A. | $({-\frac{1}{4},+∞})$ | B. | $({-\frac{1}{4},0})$ | C. | $({-\frac{1}{4},2})$ | D. | $[{-\frac{1}{4},2}]$ |
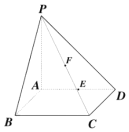 如图:在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AD=2.
如图:在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AD=2.