题目内容
1.已知双曲线Γ:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一条渐近线为l,圆C:(x-a)2+y2=8与l交于A,B两点,若△ABC是等腰直角三角形,且$\overrightarrow{OB}=5\overrightarrow{OA}$(其中O为坐标原点),则双曲线Γ的离心率为( )| A. | $\frac{{2\sqrt{13}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{5}$ | C. | $\frac{{\sqrt{13}}}{5}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
分析 求出双曲线的一条渐近线方程,圆C的圆心和半径,设OA=t,由$\overrightarrow{OB}=5\overrightarrow{OA}$,可得OB=5t,AB=4t,可得t=1,
过C作CD⊥AB,且D为AB的中点,运用直角三角形的勾股定理和点到直线的距离公式,解得a,b,c,再由离心率公式,计算即可得到所求值.
解答 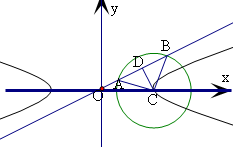 解:双曲线Γ:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一条渐近线l的方程为y=$\frac{b}{a}$x,
解:双曲线Γ:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一条渐近线l的方程为y=$\frac{b}{a}$x,
圆C:(x-a)2+y2=8的圆心C(a,0),半径为r=2$\sqrt{2}$,
由△ABC为等腰直角三角形,可得AB=$\sqrt{2}$r=4,
设OA=t,由$\overrightarrow{OB}=5\overrightarrow{OA}$,可得OB=5t,AB=4t,可得t=1,
过C作CD⊥AB,且D为AB的中点,OD=3,AB=4,AD=2,
C到直线l的距离为CD=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$,
在直角三角形OCD中,CD2=OC2-OD2,
在直角三角形ACD中,CD2=AC2-AD2,
即有a2-9=8-4,解得a=$\sqrt{13}$,
即有CD=2=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$,解得b=$\frac{2\sqrt{13}}{3}$,
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{13+\frac{52}{9}}$=$\frac{13}{3}$,
e=$\frac{c}{a}$=$\frac{\sqrt{13}}{3}$.
故选:D.
点评 本题考查双曲线的方程和性质,主要是渐近线方程和离心率的求法,考查圆的垂径定理和直角三角形的勾股定理的运用,以及向量的共线,考查化简整理的运算能力,属于中档题.

| A. | f(x)>0 | B. | f(x)<0 | C. | f(x)为减函数 | D. | f(x)为增函数 |
| A. | $({-\frac{1}{4},+∞})$ | B. | $({-\frac{1}{4},0})$ | C. | $({-\frac{1}{4},2})$ | D. | $[{-\frac{1}{4},2}]$ |
| A. | 5 | B. | -10 | C. | -32 | D. | -42 |
| A. | ?x0>0,(x0,$\frac{1}{2}$)∈D | B. | ?x0>0,(x0,$\frac{1}{2}$x0)∉D | C. | ?x0>0,(x0,$\frac{1}{2}$)∈D | D. | ?x0>0,(x0,$\frac{1}{2}$x0)∉D |
| A. | y=2x2 | B. | y=4x2 | C. | y=6x2 | D. | y=8x2 |